If each interior angle of a regular polygon is x^o and each exterior angle is

If each interior angle of a regular polygon is $x^o$ and each exterior angle is
$\frac{x - 36}{3}$
Calculate the sum of the interior angles in the polygon.

Answers

Interior angle + exterior angles =

$180^o$

$\frac{x-36}{3}$ + x = 180

$\frac{x-36+3x}{3}$ = 180

4x - 36 = 540;

4x = 576

x = 144

Exterior angle

=

$\frac{144-36}{3}$ =

$\frac{108}{3}$ =

$36^o$

the number of sides =

$\frac{360}{36}$ = 10

Sum of interior angle is

= (2n - 4)90 = (2 x 10 - 4)90

= (20 - 4)90 = 16 x 90 =

$1440^o$

x = 144

Exterior angle

=

$\frac{144-36}{3}$ =

$\frac{108}{3}$ =

$36^o$

the number of sides =

$\frac{360}{36}$ = 10

Sum of interior angles is

= (2n - 4)90 = (2 x 10 - 4)90

= (20 - 4)

$90^o$ = 16

johnmulu answered the question on June 10, 2017 at 06:22

Next: How do human activities contribute to soil erosion?
Previous: How does climate influence the formation of soil?

View More Mathematics Questions and Answers | Return to Questions Index

Exams With Marking Schemes

Related Questions

A regular polygon has its interior angle as 156^o. Find the number of sides that the polygon has. (Solved)
A regular polygon has its interior angle as 156^o. Find the number of sides that the polygon has.

Date posted: June 10, 2017. Answers (1)
The sum of interior angles of a polygon is 2880^o. Find (Solved)
The sum of interior angles of a polygon is 2880^o. Find
(a) The number of sides the polygon has.
(b) The number of triangles which can be formed when diagonals are drawn from one vertex connecting the other vertices.

Date posted: June 9, 2017. Answers (1)
Two of the interior angles of a pentagon are 100^o and 140^o. Find the remaining angles if they are all equal. (Solved)
Two of the interior angles of a pentagon are 100^o and 140^o. Find the remaining angles if they are all equal.

Date posted: June 9, 2017. Answers (1)
The figure below shows part of a regular polygon not drawn to scale. (Solved)
The figure below shows part of a regular polygon not drawn to scale.

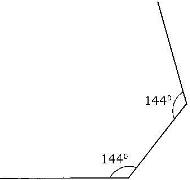
Determine the number of sides the polygon has.

Date posted: June 9, 2017. Answers (1)

Find the sum of interior angles of a regular polygon with 18 sides. (Solved)
Find the sum of interior angles of a regular polygon with 18 sides.

Date posted: June 9, 2017. Answers (1)
The angles of a quadrilateral are 3x^o, 2x^o, (x+54)^o and 2(x-7)^o. Find the smallest angle of the polygon. (Solved)
The angles of a quadrilateral are 3x^o, 2x^o, (x+54)^o and 2(x-7)^o. Find the smallest angle of the polygon.

Date posted: June 9, 2017. Answers (1)
In the figure below AB is parallel to DE, angle ABD = 30^o and angle DCE = 70^o. Giving reasons, find angle:(Solved)
In the figure below AB is parallel to DE, angle ABD = 30^o and angle DCE = 70^o. Giving reasons, find angle:
(i) CDE
(ii) CEF.

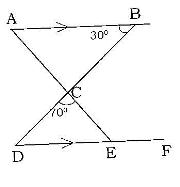
Date posted: June 9, 2017. Answers (1)
In the figure below, ABCD is a cyclic quadrilateral and BD is diagonal. EADF is straight line, CDF = 68^o, BDC = 45^o and BAE = 98^o(Solved)
In the figure below, ABCD is a cyclic quadrilateral and BD is diagonal. EADF is straight line, CDF = 68^o, BDC = 45^o and BAE = 98^o

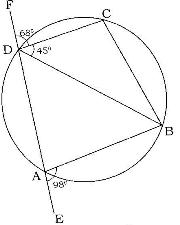
Calculate the size of
(a) CBD (b) ABD

Date posted: June 9, 2017. Answers (1)

In the figure below, AB is parallel to DE. DE bisectors angle BDG and DCF = 60^o and CFG = 110^o. (Solved)
In the figure below, AB is parallel to DE. DE bisectors angle BDG and DCF = 60^o and CFG = 110^o.
Find (a) CDF (b) ABD
Give reasons for your answer.

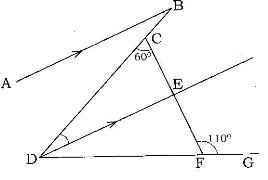
Date posted: June 9, 2017. Answers (1)
In the figure below, O is the centre of the circle and OAC = 38^o. Find (Solved)
In the figure below, O is the centre of the circle and OAC = 38^o. Find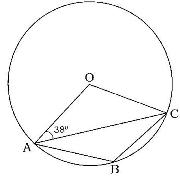

Date posted: June 9, 2017. Answers (1)

Find the value of a and b in (Solved)
Find the value of a and b in

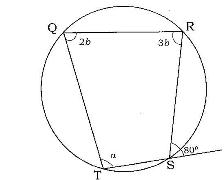
Date posted: June 9, 2017. Answers (1)
Find the value of x in the figure below. (Solved)
Find the value of x in the figure below.

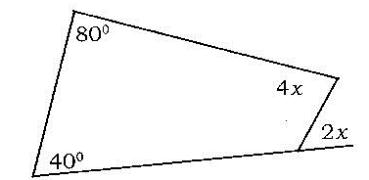
Date posted: June 9, 2017. Answers (1)
Find the value of p and y in the figure below. (Solved)
Find the value of p and y in the figure below.

Date posted: June 9, 2017. Answers (1)
The opposite angle of a cyclic quadrilateral are (5x + 40)^o and (3x - 20)^o respectively. Find the difference between the two angles. (Solved)
The opposite angle of a cyclic quadrilateral are (5x + 40)^o and (3x - 20)^o respectively. Find the difference between the two angles.

Date posted: June 9, 2017. Answers (1)
The three angles of a triangle are (x-20)^o, (4x-15)^o and (2x+5)^o. Find the difference between the largest and the smallest. (Solved)
The three angles of a triangle are (x-20)^o, (4x-15)^o and (2x+5)^o. Find the difference between the largest and the smallest.

Date posted: June 9, 2017. Answers (1)
State the co-ordinates of the points Q, R A, B and C. (Solved)
State the co-ordinates of the points Q, R A, B and C.

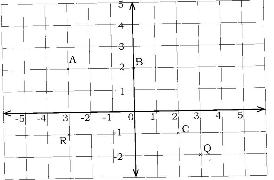
Date posted: June 9, 2017. Answers (1)
A traveller had sterling pounds 918 which he exchanged to Kenya Shillings at the rate of sh 84 per(Solved)
A traveller had sterling pounds 918 which he exchanged to Kenya Shillings at the rate of sh 84 per sterling pound. He did not spend the money as intended. Later, he used the Kenyan Shillings to buy sterling pounds at the rate of Ksh 85 per Sterling pounds at the rate of Ksh 85 per Sterling pound. Calculate the amount in sterling pounds lost in the whole transaction.

Date posted: June 9, 2017. Answers (1)
Kenyan business man owes U.S dollars 100 000 to a company in the united states of America The Kenyan can either pay through his account in the united kingdom. Which is cheaper and by how much. Give your answer in Kenyan Shillings given that; (Solved)
Kenyan business man owes U.S dollars 100 000 to a company in the united states of America The Kenyan can either pay through his account in the united kingdom. Which is cheaper and by how much. Give your answer in Kenyan Shillings given that;
1 U.S dollar
= 28.74 Shillings
I Sterling pound
= 1.79 U.S dollars
1 Sterling pound
= 50.80 Kenya Shillings

Date posted: June 9, 2017. Answers (1)
In this question, mathematical tables should not be used. A Kenyan bank buys and sells foreign currencies as shown below; (Solved)
In this question, mathematical tables should not be used. A Kenyan bank buys and sells foreign currencies as shown below;

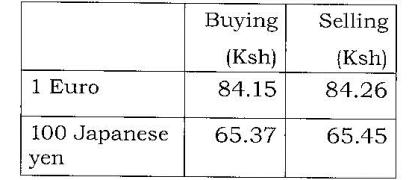
A Japanese travelling from France arrives in Kenya with 5 000 Euros. He converts all the 5000 Euros. He converts all the 5000 Euros to Kenya Shillings at the bank. While in Kenya he spends a total of sh 289 850 and then converts the remaining Kenya Shillings to Japanese yen at the bank. Calculate the amount in Japanese yen he receives.

Date posted: June 9, 2017. Answers (1)
During a certain period of the year, the rate were as follows 1 Sterling pound = Ksh 102.00 1 Sterling pound = 1.49 US dollar 1 US dollar = Ksh 60.60(Solved)
During a certain period of the year, the rate were as follows
1 Sterling pound
= Ksh 102.00
1 Sterling pound
= 1.49 US dollar
1 US dollar = Ksh 60.60

A school management intended to import textbooks worth sh 500 000 from U.K. It changed the money to sterling pound. Later the management found out that the books were cheaper in U.S. Hence it changed the sterling pounds to dollars. Unfortunately a financial crisis arose and the money had to be reconverted to Kenya Shillings. Calculate the total amount of money the management ended up with.

Date posted: June 9, 2017. Answers (1)