Consider a body moving in a straight line from an initial velocity u to a final velocity v(u, v?0) within a time t as represented on the graph below:
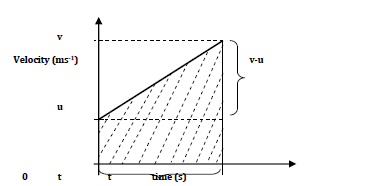
The slope of the graph represents the acceleration of the body;
Acceleration, a=(v-u)/t.
Therefore, v=u+at…………………………………. i.
This is the first equation of linear motion.
The area under the graph (area of a trapezium) gives the displacement of the body.
Hence, displacement s= ½(sum of // sides) x perpendicular height between them.
s= ½(u+v)t.
But v=u+at,
Therefore, s=½{u+(u+at)}t
s=½(2u+at)t
Hence, s=ut+½at
2……………………………. ii.
This is the second equation of linear motion.
Also, rearranging equation i, we have t=(v-u)/a. substituting this in equation ii, we obtain;
s=ut+½at
2=u{(v-u)/a}+½a{(v-u)/a}.
s=u(v-u)/a + a(v-u)
2/2a
2= u(v-u)/a + (v-u)
2/2a
s= {2u(v-u) + (v-u)
2}/2a = {2uv-2u
2+v
2+u
2-2uv}/2a
s= {v
2-u
2}/2a
2as= v
2-u
2Hence, v
2=u
2+2as ……………………………….. iii.
This is the third equation of linear motion.
The three equations hold for any body moving with uniform acceleration.
sharon kalunda answered the question on
April 23, 2019 at 09:24