Two narrow and very close slits S1 and S2 are placed infront of a monochromatic light source.
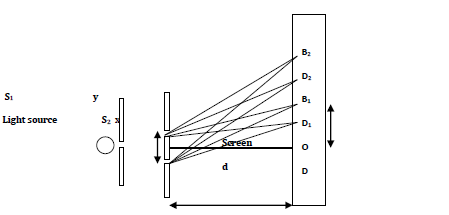
The light waves from the two slits undergo diffraction and superimpose as they spread out. A series of alternating bright and dark fringes are observed on the screen. The bright fringes are due to constructive interference while the dark fringes are due to destructive interference. However, along the central line through the centre of the slits and point O, it is bright throughout.
At O, the path difference of the two waves is zero since S1O=S2O. Moving upwards or downwards to the first bright fringe, the path difference is equivalent to one wavelength;
i.eS2B1-S1B1= 1?
At D1, the path difference is equivalent to half a wavelength;
S2D1-S1D1= 1/2?
Similarly, at the second bright fringe B2, the path difference is equivalent to two wavelengths;
i.eS2B2-S1B2= 2?
And S2D2-S1D2= 3/2?
Generally, at the nth bright fringe, the path difference will be n times the wavelength;
S2Bn-S1Bn= n?
The wavelength of the light used can also be determined from the expression below:
?= xy/d,
Where x- the slit separation,
y- Distance between successive bright fringes and
d- Perpendicular distance of the slits from the screen.
sharon kalunda answered the question on
April 24, 2019 at 10:20