- A rectangular slab of glass measures 8cm by 3cm by 2cm and has a mass of 5.5kg. Calculate the density of glass in g/cm3.(Solved)
A rectangular slab of glass measures 8cm by 3cm by 2cm and has a mass of 5.5kg. Calculate the density of glass in g/cm3.
Date posted: April 30, 2019. Answers (1)
- Use the prime factors of 3136 and 2744 to evaluate:(Solved)
Use the prime factors of 3136 and 2744 to evaluate:
Date posted: April 30, 2019. Answers (1)
- Evaluate using logarithms(Solved)
Evaluate using logarithms
Date posted: April 30, 2019. Answers (1)
- In the figure below,DE=1/2AB,BC=2/3BD and the coordinates of A, B and D are (5, 4), (9, 6) and (12, 0) respectively.(Solved)
In the figure below,DE=1/2AB,BC=2/3BD and the coordinates of A, B and D are (5, 4), (9, 6) and (12, 0) respectively.
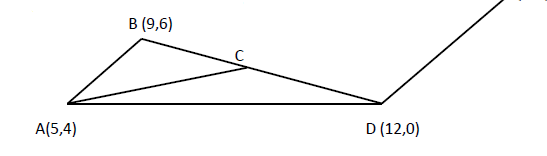
Find the column vectors:
i) BD
ii) BC
iii) CD
iv) AC
Date posted: April 30, 2019. Answers (1)
- Solve for theta in the equation 3 cos2theta + sin theta + 1 = 0 0 = theta = 3600(Solved)
Solve for theta in the equation 3 cos2theta + sin theta + 1 = 0 0 ≤ theta ≤ 3600
Date posted: April 30, 2019. Answers (1)
- a)Draw the graph of the function y = 1 + x -2x2 on the graph paper provided.(Solved)
a)Draw the graph of the function y = 1 + x -2x2 on the graph paper provided.
b) Use your graph to find the value for x in the equation 1 + x -2x2 = 0
c) By drawing a suitable line graph on the same graph find the value for x which satisfies the equation 2 + 2x- 2x2 = 0
Date posted: April 30, 2019. Answers (1)
- An aircraft leaves town P ( 30oS, 17oE) and moves directly northwards to Q(60°N, 17°E). It then moved at an average speed of 300 knots...(Solved)
An aircraft leaves town P ( 30oS, 17oE) and moves directly northwards to Q(60°N, 17°E). It then moved at an average speed of 300 knots for 8 hours westwards to town R. Determine;
a) The distance PQ in nautical miles.
b) The position of town R.
c) The local time at R if local time at Q is 3.12p.m
d) The total distance moved from P to R in kilometers. Take 1 nautical; = 1.853 kilometres.
Date posted: April 30, 2019. Answers (1)
- A particle P moves in a straight line so that its velocity, V m/s at time t = 0 seconds t is given by V...(Solved)
A particle P moves in a straight line so that its velocity, V m/s at time t ≥ 0 seconds t is given by V = 28 + t – 2t2. Find.
a) The time when p is momentarily at rest.
b) The speed of P at the instant when the acceleration of the particles is zero.
c) Given that P passes through the point O of the line when t = 0, find the distance of P from O when P is momentarily
at rest.
Date posted: April 30, 2019. Answers (1)
- Every evening before the end of preps, Eunice either reads a novel or solves a mathematical problem. The probability
that she reads a novel is 4/5.If...(Solved)
Every evening before the end of preps, Eunice either reads a novel or solves a mathematical problem. The probability
that she reads a novel is 4/5.If she read a novel, there is a probability of 3/4 that she will fall asleep. If he solves a mathematical problem, there is a probability of 1/4 that she will fall asleep. Sometimes the teacher on duty enters Eunice’s classroom. When Eunice is asked whether she had been asleep, there is a probability of only 1/5 that she will
admit that she had been asleep and a probability of 3/5 that she will claim to have been asleep when she had not been asleep
By use of a tree diagram, find the probability that
a) She sleeps and admits
b) She sleeps and does not admit
c). She does not sleep but claims that she had been asleep
d). She does not sleep and says that she has not been asleep
Date posted: April 30, 2019. Answers (1)
- A man sold a plot of land for sh. 160,000 and invested the money in a bank which pays 12% p.a. compounded semiannually.
After 2 years,...(Solved)
A man sold a plot of land for sh. 160,000 and invested the money in a bank which pays 12% p.a. compounded semiannually.
After 2 years, he withdrew sh. 100,000 and the left the rest for a further 3 years.
a) How much did she leave in the bank at the end of 2 years?
b) How much did he have in the bank at the end of 5 years?
c) Calculate the total interest made for the whole period.
Date posted: April 30, 2019. Answers (1)
- The first three terms of a geometric series are 2x,x- 8 and 2x+ 5 respectively.(Solved)
The first three terms of a geometric series are 2x,x− 8 and 2x+ 5 respectively.
a) Find the possible values of x.
b) For the value of x being an integer, find:
i) The value of the eleventh term
ii) The sum of the first 15 terms
Date posted: April 30, 2019. Answers (1)
- Two tanks of equal volume are connected in such a way that one tank can be filled by pipe A in 1 hour 20 minutes....(Solved)
Two tanks of equal volume are connected in such a way that one tank can be filled by pipe A in 1 hour 20 minutes. Pipe
B can drain one tank in 3hours 36 minutes but pipe C alone can drain both tanks in 9 hours. Calculate:
(a) The fraction of one tank that can be filled by pipe A in one hour.
(b) The fraction of one tank that can be drained by both pipes B and C in one hour.
(c) Pipe A closes automatically once both tanks are filled. Assuming that initially both tanks are empty and all pipes
opened at once, calculate how long it takes before pipe A closes.
Date posted: April 30, 2019. Answers (1)
- In the figure below, PQRST right pyramid on a rectangular base. Point O is vertically below P, QR = 24cm, RS = 10cm
and RP =...(Solved)
In the figure below, PQRST right pyramid on a rectangular base. Point O is vertically below P, QR = 24cm, RS = 10cm
and RP = 26cm. Calculate the angle the plane RSP makes with the base.
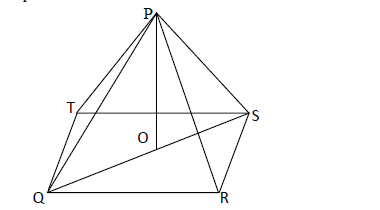
Date posted: April 30, 2019. Answers (1)
- An object of an area 4cm2 is mapped onto an area 64cm2 under the transformation of matrix below. Find the possible values of n.(Solved)
An object of an area 4cm2 is mapped onto an area 64cm2 under the transformation of matrix below. Find the possible values of n.
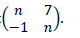
Date posted: April 30, 2019. Answers (1)
- If r = 3i – j + k and t = j + 2k. P = r -2t find |P| to 4 s.f.(Solved)
If r = 3i – j + k and t = j + 2k. P = r -2t find |P| to 4 s.f.
Date posted: April 30, 2019. Answers (1)
- Give that x2 + 6x +y2 – 8y - 11= 0 is the equation of a circle, find the centre and the radius of the...(Solved)
Give that x2 + 6x +y2 – 8y - 11= 0 is the equation of a circle, find the centre and the radius of the circle.
Date posted: April 30, 2019. Answers (1)
- Find the equation of the normal of the curve. y = x5 + 3x2 + 5x at the point (1,3)(Solved)
Find the equation of the normal of the curve. y = x5 + 3x2 + 5x at the point (1,3)
Date posted: April 30, 2019. Answers (1)
- Without using a calculator or mathematical tables, express;(Solved)
Without using a calculator or mathematical tables, express;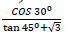
in surd form and simplify Leaving your answer in the form a+ b √c where a, b, and c are rational numbers.
Date posted: April 30, 2019. Answers (1)
- a) Expand and simplify the binominal expression ( 2+ 2y)5 in ascending powers of y (Solved)
a) Expand and simplify the binominal expression ( 2+ 2y)5 in ascending powers of y
b) Use the expansion up to the fourth term to evaluate (2.02)5 correct to 4 decimal places.
Date posted: April 30, 2019. Answers (1)
- A shear parallel to the x-axis maps point (1,2) onto a point (5, 2) .Determine the shear factors and hence state the shear matrix (invariant...(Solved)
A shear parallel to the x-axis maps point (1,2) onto a point (5, 2) .Determine the shear factors and hence state the shear matrix (invariant line is y = 0)
Date posted: April 30, 2019. Answers (1)