- A polygon of n sides has half of the interior angles 1500 each and the rest 1700 each. Find the value of n.(Solved)
A polygon of n sides has half of the interior angles 1500 each and the rest 1700 each. Find the value of n.
Date posted: May 3, 2019. Answers (1)
- If 2/3 is added to the numerator of a certain fraction the fraction will be increased by 1/21 and if 1/2 is deducted
from its denominator...(Solved)
If 2/3 is added to the numerator of a certain fraction the fraction will be increased by 1/21 and if 1/2 is deducted
from its denominator that fraction becomes 2/9. Find the reciprocal of the fraction.
Date posted: May 3, 2019. Answers (1)
- Simplify the expression.(Solved)
Simplify the expression.

Hence solve the equation

Date posted: May 3, 2019. Answers (1)
- Simplify completely(Solved)
Simplify completely

Date posted: May 3, 2019. Answers (1)
- The position of two towns A and B on earth surface are (360N, 490E) and (360N, 1310W) respectively.Take R = 6370(Solved)
The position of two towns A and B on earth surface are (360N, 490E) and (360N, 1310W) respectively.Take R = 6370
a) Find the difference in longitude between the town A and B.
b) Calculate the distance between A and B along the latitude in
i) nautical miles
ii) kilometres
c) i) Another town C is 840km East of town B and on the same latitude as town A and B . Find the position of town C.
ii) If the local time in B is 7.30 a.m, find the local time in C.
Date posted: May 3, 2019. Answers (1)
- A particle moving along a line passes a point O at a velocity of 15m/s and its acceleration t seconds later is given by
a=...(Solved)
A particle moving along a line passes a point O at a velocity of 15m/s and its acceleration t seconds later is given by
a= (2t - 8) m/s2
a) Find the expression of the velocity after passing the point O.
b) Find the time when the particle is at rest.
c) Find the distance between the points when the particle is at rest.
Date posted: May 3, 2019. Answers (1)
- The first, third and sixth terms of an arithmetic progression (AP) correspond to the first three consecutive terms of a
geometric progression (GP). The first term...(Solved)
The first, third and sixth terms of an arithmetic progression (AP) correspond to the first three consecutive terms of a
geometric progression (GP). The first term of each progression is 16, common difference of AP and d and common
ratio of the GP is r.
a) i) Write two equations involving d and r.
ii) Find the values of d and r.
b) Find the sum of the first 20 terms in the
i) Arithmetic progression (AP).
ii) Geometric progression (GP)
Date posted: May 3, 2019. Answers (1)
- The probability of three dart players Githongo, Mwai and Kanyoro hitting the bulls eye in a competition are 0.4, 0.7
and 0.5 respectively.(Solved)
The probability of three dart players Githongo, Mwai and Kanyoro hitting the bulls eye in a competition are 0.4, 0.7
and 0.5 respectively.
a) Draw a probability tree diagrams to show the possible outcomes.
b) Find the probability that
i) all hit the bulls eye.
ii) only one of them hit the bulls eye.
iii) atmost one missed the bulls eye.
Date posted: May 3, 2019. Answers (1)
- A company is to construct a parking bay whose area is 135m2. It is to be covered with a concrete slab of uniform
thickness of 150mm....(Solved)
A company is to construct a parking bay whose area is 135m2. It is to be covered with a concrete slab of uniform
thickness of 150mm. To make the slab, cement, ballast and sand are to be mixed so that their masses are in the ratio 1 :4 : 4. The mass of 1m3 of dry slab is 2500kg. Calculate
a) i) the volume of the slab.
ii) the mass of the dry slab.
iii) the mass of cement to be used.
b) If one bag of cement is 50kg, find the number of bags to be purchased.
c) If a lorry carries 7 tonnes of sand, calculate the number of lorries of sand to be purchased.
Date posted: May 3, 2019. Answers (1)
- Mr. Kamau borrowed some money at 8% simple interest p.a. He borrowed the same amount and again repaid at the
end of the year. If Kamau...(Solved)
Mr. Kamau borrowed some money at 8% simple interest p.a. He borrowed the same amount and again repaid at the
end of the year. If Kamau paid interest of Ksh. 2500 and ksh. 4000 respectively for each year, calculate
a) The value of r
b) The amount borrowed per year.
Date posted: May 3, 2019. Answers (1)
- Two quantities A and B are such that B varies directly as square of A. When A is increased by 20%, what percentage
increase in B.(Solved)
Two quantities A and B are such that B varies directly as square of A. When A is increased by 20%, what percentage
increase in B.
Date posted: May 3, 2019. Answers (1)
- Use method of completing of square leaving your answer in a simplified surds x2 = 7x - 2(Solved)
Use method of completing of square leaving your answer in a simplified surds x2 = 7x - 2
Date posted: May 3, 2019. Answers (1)
- Given matrices A and C as follows;(Solved)
Given matrices A and C as follows;


Find a matrix B so that BA = c
Date posted: May 3, 2019. Answers (1)
- Find the value of x in the equation 10Cos2x - 7sinx + 2 = 0 for domain 00= x = 3600.(Solved)
Find the value of x in the equation 10Cos2x - 7sinx + 2 = 0 for domain 00≤ x ≤ 3600.
Date posted: May 3, 2019. Answers (1)
- Simplify the following expression as far as possible.(Solved)
Simplify the following expression as far as possible.

Hence or otherwise simplified
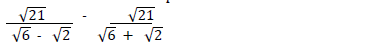
Date posted: May 3, 2019. Answers (1)
- The vectors a = (2x - 4)i + (x - 3)j + (x - 2)k and the length of /a/ = 7. Find two possible...(Solved)
The vectors a = (2x - 4)i + (x - 3)j + (x - 2)k and the length of /a/ = 7. Find two possible values of x.
Date posted: May 3, 2019. Answers (1)
- Given that (x - 2) is a factor of 3x2 + kx - 2 find the value of k and hence the other factor.(Solved)
Given that (x - 2) is a factor of 3x2 + kx - 2 find the value of k and hence the other factor.
Date posted: May 3, 2019. Answers (1)
- a) Expand and simplified the first four terms of the binomial expression (2 - 3x)6.(Solved)
a) Expand and simplified the first four terms of the binomial expression (2 - 3x)6.
b) Use the simplified expression in (a) above to estimate the value of (1.97)6 correct 5 decimal places.
Date posted: May 3, 2019. Answers (1)
- Two values X and Y are such that
3.5 < x < 4.9
0.03 < y < 0.27
What is the greatest possible value of x2/y(Solved)
Two values X and Y are such that
3.5 ≤ x ≤ 4.9
0.03 ≤ y ≤ 0.27
What is the greatest possible value of x2/y
Date posted: May 3, 2019. Answers (1)
- The equation of a circle is x2 - 8x + y2 + 12y = 12. Determine the centre and its radius of the circle.(Solved)
The equation of a circle is x2 - 8x + y2 + 12y = 12. Determine the centre and its radius of the circle.
Date posted: May 3, 2019. Answers (1)