- a) Expand (1 – 2x)6 upto to the fourth term.(Solved)
a) Expand (1 – 2x)6 upto to the fourth term.
b) Use the expansion in (a) above to find the value of (0.98)6 correct to 4 significant figures.
Date posted: May 7, 2019. Answers (1)
- The base and the height of a right angled triangle were measured as 4.34 cm and 8.25 cm respectively.Calculate the percentage error in the area...(Solved)
The base and the height of a right angled triangle were measured as 4.34 cm and 8.25 cm respectively.Calculate the percentage error in the area of the triangle.
Date posted: May 7, 2019. Answers (1)
- Simplify the expression.(Solved)
Simplify the expression.

Date posted: May 7, 2019. Answers (1)
- Solve for x and y given that.(Solved)
Solve for x and y given that.

Date posted: May 7, 2019. Answers (1)
- A sum of sh. 50,000 is invested in a financial institution that gives 12% p.a. Find the total investment after 3 years if
the interest is...(Solved)
A sum of sh. 50,000 is invested in a financial institution that gives 12% p.a. Find the total investment after 3 years if
the interest is compounded quarterly. Give your answer to the nearest 100.
Date posted: May 7, 2019. Answers (1)
- Find the interquartile range of the data below:
2,4,6,8,10,5,6,9,4,6(Solved)
Find the interquartile range of the data below:
2,4,6,8,10,5,6,9,4,6
Date posted: May 7, 2019. Answers (1)
- Solve for x in the equation. Sin (2x – 10)0 = -0.5 for 00= x= 3600(Solved)
Solve for x in the equation. Sin (2x – 10)0 = -0.5 for 00≤ x≤ 3600
Date posted: May 7, 2019. Answers (1)
- In the triangle below, a point R moves such that the area of ? ACB = area of ? ARB and < ARB = 300....(Solved)
In the triangle below, a point R moves such that the area of Δ ACB = area of Δ ARB and < ARB = 300. Using a ruler and
a pair of compasses only, locate the possible position of R on the same side as C and find the distance between them.
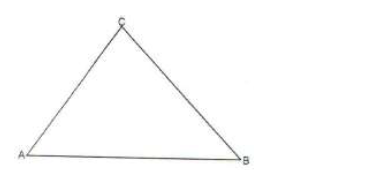
Date posted: May 7, 2019. Answers (1)
- A point divides line PQ in the ratio 3: -2. Given that P = 2i -3j + k and Q = 3i -4j – 3k...(Solved)
A point divides line PQ in the ratio 3: -2. Given that P = 2i -3j + k and Q = 3i -4j – 3k find the coordinates of T.
Date posted: May 7, 2019. Answers (1)
- Make x the subject of the formula(Solved)
Make x the subject of the formula

Date posted: May 7, 2019. Answers (1)
- Use logarithm tables to evaluate:(Solved)
Use logarithm tables to evaluate:

Date posted: May 7, 2019. Answers (1)
- In the figure below, AT and AD are tangents to the circle at B and D respectively. DEF is a straight line, < ?????? =...(Solved)
In the figure below, AT and AD are tangents to the circle at B and D respectively. DEF is a straight line, < 𝐶𝐵𝑇 = 600, 0 and < ADF = 420
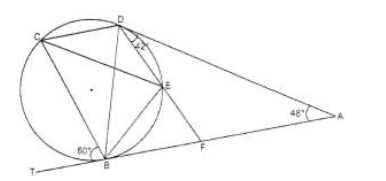
Calculate giving reasons, the value of:
a) < DCE
b) c) d) e)
Date posted: May 6, 2019. Answers (1)
- A pole stands directly across the street from a building. The angle of depression of the top of the building from the top
of the pole...(Solved)
A pole stands directly across the street from a building. The angle of depression of the top of the building from the top
of the pole is 24.50 and the angle of elevation of the top of the pole from the foot of the building is 48.60. Given that the
distance between the pole and the building is 50 m, calculate to 2 decimal places.
a) the height of the pole
b) the difference in height between the pole and the building.
c) the height of the building.
d) the angle of elevation of the top of the building from the top of the pole.
Date posted: May 6, 2019. Answers (1)
- A triangular plot PQR is such that PQ = 72m, QR = 80m and PR = 84m(Solved)
A triangular plot PQR is such that PQ = 72m, QR = 80m and PR = 84m
calculate.
i) the area of the plot in square metres
ii) the largest angle in the triangle
iii) The perpendicular height from P to the side QR
Date posted: May 6, 2019. Answers (1)
- The velocity of a particle moving in a straight line after t seconds is given by V = 2t2 – t-6m/s. calculate(Solved)
The velocity of a particle moving in a straight line after t seconds is given by V = 2t2 – t-6m/s. calculate
a) the acceleration of particle after 2 seconds
b) the distance covered during the third second.
c) the time when the particle will be momentarily at rest.
d) the minimum velocity attained.
Date posted: May 6, 2019. Answers (1)
- A hotel planned to buy sacks of charcoal for a total of sh. 30,000. Before the hotel could buy the charcoal, the price per
sack was...(Solved)
A hotel planned to buy sacks of charcoal for a total of sh. 30,000. Before the hotel could buy the charcoal, the price per
sack was reduced by sh. 100. This reduction in price enabled the hotel to buy 10 more sacks of charcoal.
a) Determine the number of sacks that the hotel bought.
b) Calculate the percentage change in price
c) If the charcoal dealer makes sh. 50 per bag as commission, calculate the total commission.
Date posted: May 6, 2019. Answers (1)
- i) It would take Alex working alone 30 days, Bernard 40 days and Charles 60 days to complete a task. All three start
working together but...(Solved)
i) It would take Alex working alone 30 days, Bernard 40 days and Charles 60 days to complete a task. All three start
working together but after five days, Alex falls sick and cannot continue. Determine how many more days it will take
Bernard and Charles to complete the task.
ii) A dealer has three grades of coffee, A, B and C. Grade A costs sh. 140 per kg., grade B costs sh.16 per kg and grade C
cost sh. 256 per kg.
a) The dealer mixes grade A and B in the ratio 5:3 to make a brand of coffee which he sells at sh. 180 per kg. Calculate
the percentage profit he makes.
b) The dealer maker a new brand by mixing the three grades of coffee in three in the ratio A: B = 5:3 and B: C = 2:5.
Determine the selling price of the new brand if he has to make a 30% profit.
Date posted: May 6, 2019. Answers (1)
- The figure below represents a solid cuboid ABCDEFGH with a rectangular base. AC = 13 cm, BC = 5 cm and CH = 15cm. M...(Solved)
The figure below represents a solid cuboid ABCDEFGH with a rectangular base. AC = 13 cm, BC = 5 cm and CH = 15cm. M is the midpoint of GH.
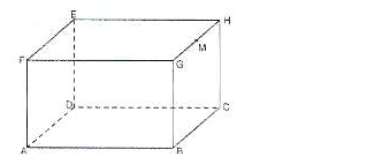
a) Calculate the surface area of the cuboid
b) Calculate the angle between line AH and the base ABCD.
c) Calculate the angle between the base ABCD and the plane ADM
d) Calculate the angle between line AC and MF
Date posted: May 6, 2019. Answers (1)
- A two digit number is such that the sum of the digits is 11. When the digits are reversed, the new number exceeds the
original number...(Solved)
A two digit number is such that the sum of the digits is 11. When the digits are reversed, the new number exceeds the
original number by 9. Calculate the original number.
Date posted: May 6, 2019. Answers (1)
- The figure below represents a solid regular hexagon based pyramid of side 4cm and height 10 cm. It is cut along a
plane 3 cm from...(Solved)
The figure below represents a solid regular hexagon based pyramid of side 4cm and height 10 cm. It is cut along a
plane 3 cm from the vertex. Calculate the volume of the remaining part.
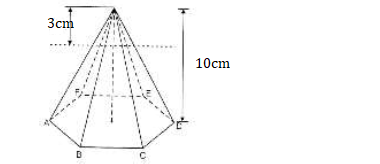
Date posted: May 6, 2019. Answers (1)