- a) Complete the table below for y = 2 Sin 2x and y = 3 Cos x.(Solved)
a) Complete the table below for y = 2 Sin 2x and y = 3 Cos x.

b) Draw the graph y = 2 Sin 2x and y = 3 Cos x using 1cm to represent 30° horizontal axis and 2cm to represent unit
on the vertical axis.
c) Use the graph to
i) solve 2 Sin x - 3 Cos x = 0
ii) Find the amplitude and period of the curve y = 2 Sin 2x.
Date posted: May 9, 2019. Answers (1)
- A variable P varies as the square of R and inversely at T.(Solved)
A variable P varies as the square of R and inversely at T.
i) When R is increased by 20%, T is reduced by 10%. Find the percentage change in value of R.
ii) When P = 12, R = 6, T=9. Find the law connecting P, R and T.
Date posted: May 9, 2019. Answers (1)
- The volume of a solid varies partly as a constant and partly as the square of the radius of its base. When volume
(v) is 95cm³,...(Solved)
The volume of a solid varies partly as a constant and partly as the square of the radius of its base. When volume
(v) is 95cm³, its radius (r) is 5cm. When its volume is 167cm³, its radius is 7cm. Find the volume when its radius is
10cm.
Date posted: May 9, 2019. Answers (1)
- The first, the 7th and the 25th terms of an arithmetic progression are the first three consecutive terms of a geometrical progression. The 20th term...(Solved)
The first, the 7th and the 25th terms of an arithmetic progression are the first three consecutive terms of a geometrical progression. The 20th term of the arithmetic progression is 22. Find:
a) i) The first term and common difference of the arithmetic progression.
ii) The sum of the first 40 terms of the arithmetic progression.
b) i) The 10th term of the geometric progression.
ii) The sum of the first 10 terms of the geometric progression.
Date posted: May 9, 2019. Answers (1)
- Two businessmen P and Q invested shs 2,400,000 each in separate banks. P invested in a bank which paid an interest
of 12% p.a. compounded semi-annually....(Solved)
Two businessmen P and Q invested shs 2,400,000 each in separate banks. P invested in a bank which paid an interest
of 12% p.a. compounded semi-annually. While Q invested in a bank which paid simple interest of 20% p.a.
a) Find:
i) the compound interest earned by P after 10 years to the nearest hundreds.
ii) the total interest earned by Q after 10 years to the nearest hundreds.
b) How long will it take P to get an amount equivalent to Kshs 6,000,000.
c) How long does it take Q to reach the amount of Kshs 6,000,000
Date posted: May 9, 2019. Answers (1)
- Income tax on all income earned were taxed as follows.(Solved)
Income tax on all income earned were taxed as follows.
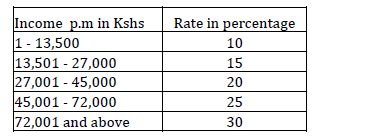
John earns a monthly salary of shs 62,400. He is entitled to a family relief of 1,056 p.m. Find his net tax p.m in kshs.
Date posted: May 9, 2019. Answers (1)
- On the line below, draw the locus of P on the upper side of AB such that angle APB is 65°(Solved)
On the line below, draw the locus of P on the upper side of AB such that angle APB is 65°

Date posted: May 9, 2019. Answers (1)
- The cost of two brands of coffee A and B are shs 120 and shs 150 per kg respectively. If A and B are mixed...(Solved)
The cost of two brands of coffee A and B are shs 120 and shs 150 per kg respectively. If A and B are mixed in ratio 3 : 7
respectively, and the selling price of the mixture is 30% above the cost, find the selling price per 500g packet of coffee.
Date posted: May 9, 2019. Answers (1)
- P(60°N, 32°E) and Q(60°N, 118°W). Find the shortest distance along parallel latitude PQ.(Solved)
P(60°N, 32°E) and Q(60°N, 118°W). Find the shortest distance along parallel latitude PQ.
Date posted: May 9, 2019. Answers (1)
- Find the percentage error in calculating the volume of the cuboid whose dimensions are 8.2cm by 6.2cm by 5.7cm(Solved)
Find the percentage error in calculating the volume of the cuboid whose dimensions are 8.2cm by 6.2cm by 5.7cm
Date posted: May 9, 2019. Answers (1)
- Find the centre and radius of a circle whose equation is given as :
2x² + 2y² + 8x - 20y = 40(Solved)
Find the centre and radius of a circle whose equation is given as :
2x² + 2y² + 8x - 20y = 40
Date posted: May 9, 2019. Answers (1)
- Solve the equation: 2 Cos 2x = v3 for 0° = x = 360°(Solved)
Solve the equation: 2 Cos 2x = √3 for 0° ≤ x ≤ 360°
Date posted: May 9, 2019. Answers (1)
- Expand and simplify (2 - x)5 hence evaluate 1.985 using the first 4 terms of the expansion.(Solved)
Expand and simplify (2 - x)5 hence evaluate 1.985 using the first 4 terms of the expansion.
Date posted: May 9, 2019. Answers (1)
- The probability of three students John, Ken and Faith passing exam are 0.8, 0.7 and 0.6 respectively. Find the
probability of any two of them passing...(Solved)
The probability of three students John, Ken and Faith passing exam are 0.8, 0.7 and 0.6 respectively. Find the
probability of any two of them passing exam.
Date posted: May 9, 2019. Answers (1)
- In the figure blow, DC is the tangent of the circle at D. BC = 8cm, AF = 6cm, DF=8cm and FE=3cm. Find the length...(Solved)
In the figure blow, DC is the tangent of the circle at D. BC = 8cm, AF = 6cm, DF=8cm and FE=3cm. Find the length FB
and DC.

Date posted: May 9, 2019. Answers (1)
- OA = 2i + 3j + 4k while OB = 5i + 9j - 2k. P divides AP externally in the ratio 2 : 1....(Solved)
OA = 2i + 3j + 4k while OB = 5i + 9j - 2k. P divides AP externally in the ratio 2 : 1. Find he coordinates of P.
Date posted: May 9, 2019. Answers (1)
- Find the value of k if 4x² + 25x + 5 + k is a perfect square.(Solved)
Find the value of k if 4x² + 25x + 5 + k is a perfect square.
Date posted: May 9, 2019. Answers (1)
- Using mid-ordinate rule of 5 strips, determine the area under the curve y = 3x² + 10, the lines x = 1, x=6 and x-axis.(Solved)
Using mid-ordinate rule of 5 strips, determine the area under the curve y = 3x² + 10, the lines x = 1, x=6 and x-axis.
Date posted: May 9, 2019. Answers (1)
- The triangle ABC below is such that AB = b and AC=c. M is on AB such that 3AM = AB and N is on...(Solved)
The triangle ABC below is such that AB = b and AC=c. M is on AB such that 3AM = AB and N is on AC such that AC: NC= 4 : 1

a) Write the following in terms of b and c
i) BC
ii)MN
iii)BN
b) Given further that BC produced intersects MN produced at L and ML = hMN while BL = kBC where h and k are
constants write ML in two ways hence find the values of h and k.
c) Show the M, N and L are collinear.
Date posted: May 9, 2019. Answers (1)
- a) Sketch the curve y = -2x² - 4x + 6 (Solved)
a) Sketch the curve y = -2x² - 4x + 6
b) Use trapezium rule taking intervals of 0.5 units to find the area under the curve.
y = -2x² - 4x + 6 within the range -2 ≤ x ≤ 4.
c) Obtain the exact area in (b) above hence calculate the percentage error introduced by using the Trapezium rule.
Date posted: May 9, 2019. Answers (1)