- Use reciprocal tables to find the reciprocals of 0.4346 and 0.9182.Hence, evaluate
(Solved)
Use reciprocal tables to find the reciprocals of 0.4346 and 0.9182.Hence, evaluate
Date posted: May 9, 2019. Answers (1)
- Two churches have a total of 500 members, the difference between members of the two churches is 200. How many
members are there in each church...(Solved)
Two churches have a total of 500 members, the difference between members of the two churches is 200. How many
members are there in each church ?
Date posted: May 9, 2019. Answers (1)
- The angle of elevation of the top of a tree from a boy’s eye positioned at point A is 20o. The boy moves 100 metres
closer...(Solved)
The angle of elevation of the top of a tree from a boy’s eye positioned at point A is 20o. The boy moves 100 metres
closer to the tree and the angle of elevation becomes 32o. Find the height of the tree. (Disregard the height of the boy)
Date posted: May 9, 2019. Answers (1)
- Write down the three inequalities which define the region R.(Solved)
Write down the three inequalities which define the region R.
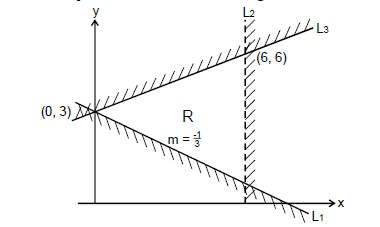
Date posted: May 9, 2019. Answers (1)
- The figure below represents a net with a path marked on it, drawn accurately.(Solved)
The figure below represents a net with a path marked on it, drawn accurately.
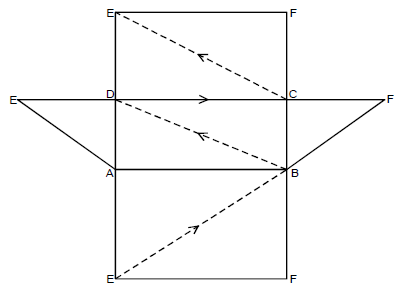
a) What solid does the net represent?
b) Draw the solid and clearly show the path.
Date posted: May 9, 2019. Answers (1)
- Solve for x and y in the equation.(Solved)
Solve for x and y in the equation.
Date posted: May 9, 2019. Answers (1)
- A line P has its x and y intercept as -2 and -3 respectively.(Solved)
A line P has its x and y intercept as -2 and -3 respectively.
a) Find the gradient of line P.
b) Line Q passes through (5, -2) and is parallel to line P. Write the equation of line Q in the form y = mx + c
Date posted: May 9, 2019. Answers (1)
- The figure below represents a swimming pool. Calculate the volume of the swimming pool in litres.(Solved)
The figure below represents a swimming pool. Calculate the volume of the swimming pool in litres.
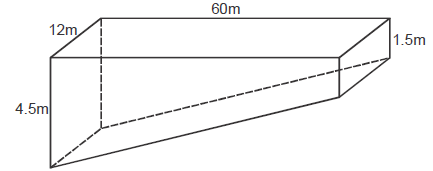
Date posted: May 9, 2019. Answers (1)
- Two types of coffee cost sh.250 per kg and sh.200 per kg are mixed so that their masses are in the ratio 3: 5
respectively. Otieno...(Solved)
Two types of coffee cost sh.250 per kg and sh.200 per kg are mixed so that their masses are in the ratio 3: 5
respectively. Otieno sold the mixture at sh.262.50. Calculate his percentage profit.
Date posted: May 9, 2019. Answers (1)
- Two towns A and B are 220km apart. A bus left town A at 11.00a.m and travelled towards town B at 60km/h. At the
same time,...(Solved)
Two towns A and B are 220km apart. A bus left town A at 11.00a.m and travelled towards town B at 60km/h. At the
same time, a matatu left town B for town A and travelled at 80km/h. The matatu stopped for 45 minutes on the way
before meeting the bus. Calculate the distance covered by the bus before meeting the matatu.
Date posted: May 9, 2019. Answers (1)
- Simplify the expression given below(Solved)
Simplify the expression given below
Date posted: May 9, 2019. Answers (1)
- Evaluate the expression below(Solved)
Evaluate the expression below
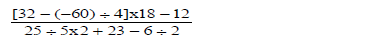
Date posted: May 9, 2019. Answers (1)
- The figure below represents a solid when is partly a cuboid and partly a right pyramid with rectangular base and
measurements as shown below.(Solved)
The figure below represents a solid when is partly a cuboid and partly a right pyramid with rectangular base and
measurements as shown below.
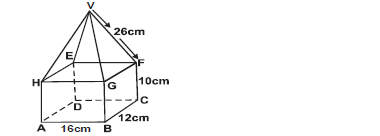
a) Determine the length AF.
b) Find the vertical height of the pyramid part.
c) Find the angle:
i) HV makes with the base ABCD
ii) HEV makes with the base HGFE.
iii) AF makes with base ABCD
Date posted: May 9, 2019. Answers (1)
- The distance (s) moved by a particle after t (seconds) is given as S=6t² - t³+ 9t metres. Determine(Solved)
The distance (s) moved by a particle after t (seconds) is given as S=6t² - t³+ 9t metres. Determine
i) Displacement after 2 seconds.
ii) The time when the particle is momentarily at rest.
iii) The velocity when t = 5 seconds
Date posted: May 9, 2019. Answers (1)
- The gradient of a curve is given as 6x² + 8x + 5. If the curve passes through (1, 28), determine the equation of the
curve.(Solved)
The gradient of a curve is given as 6x² + 8x + 5. If the curve passes through (1, 28), determine the equation of the
curve.
Date posted: May 9, 2019. Answers (1)
- A triangle ABC has vertices A(2, 1), B(5, 1) and C(4, -2). A1 (4, 1) B1(10, 1) and C1(8, -2) is the image of triangle...(Solved)
A triangle ABC has vertices A(2, 1), B(5, 1) and C(4, -2). A1 (4, 1) B1(10, 1) and C1(8, -2) is the image of triangle ABC
under a given transformation.
a) Determine a single matrix of transformation that maps ABC onto A1B1C1 hence describe fully the matrix of
transformation.
b) A²B²C² is the image of ABC under positive 90° about the origin. Determine the co-ordinates of vertices A²B²C² on the
grid provided.
c) A³B³C³ is the image of A1B1C1 under a transformation given by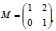
. Determine the co-ordinates of the vertices
A³B³C³.
Date posted: May 9, 2019. Answers (1)
- a) Complete the table below for y = 2 Sin 2x and y = 3 Cos x.(Solved)
a) Complete the table below for y = 2 Sin 2x and y = 3 Cos x.
b) Draw the graph y = 2 Sin 2x and y = 3 Cos x using 1cm to represent 30° horizontal axis and 2cm to represent unit
on the vertical axis.
c) Use the graph to
i) solve 2 Sin x - 3 Cos x = 0
ii) Find the amplitude and period of the curve y = 2 Sin 2x.
Date posted: May 9, 2019. Answers (1)
- A variable P varies as the square of R and inversely at T.(Solved)
A variable P varies as the square of R and inversely at T.
i) When R is increased by 20%, T is reduced by 10%. Find the percentage change in value of R.
ii) When P = 12, R = 6, T=9. Find the law connecting P, R and T.
Date posted: May 9, 2019. Answers (1)
- The volume of a solid varies partly as a constant and partly as the square of the radius of its base. When volume
(v) is 95cm³,...(Solved)
The volume of a solid varies partly as a constant and partly as the square of the radius of its base. When volume
(v) is 95cm³, its radius (r) is 5cm. When its volume is 167cm³, its radius is 7cm. Find the volume when its radius is
10cm.
Date posted: May 9, 2019. Answers (1)
- The first, the 7th and the 25th terms of an arithmetic progression are the first three consecutive terms of a geometrical progression. The 20th term...(Solved)
The first, the 7th and the 25th terms of an arithmetic progression are the first three consecutive terms of a geometrical progression. The 20th term of the arithmetic progression is 22. Find:
a) i) The first term and common difference of the arithmetic progression.
ii) The sum of the first 40 terms of the arithmetic progression.
b) i) The 10th term of the geometric progression.
ii) The sum of the first 10 terms of the geometric progression.
Date posted: May 9, 2019. Answers (1)