-
A triangle PQR whose vertices are P(2, 2), Q(5, 3) and R(4, 1) is mapped onto triangle P1Q1R1 by a transformation
whose matrix is
(Solved)
A triangle PQR whose vertices are P(2, 2), Q(5, 3) and R(4, 1) is mapped onto triangle P1Q1R1 by a transformation
whose matrix is

a) On the grid provided below, draw triangle PQR and triangle P1Q1R1
b) Triangle P1Q1R1 is mapped onto a triangle whose vertices are P11(-2, -2), Q11(-5, -3) and R11(-4, -1)
i) Draw triangle P11Q11R11 on the same grid.
ii) Find the matrix representing transformation that maps triangle P1Q1R1 onto triangle P11Q11R11
c) Describe the transformation that maps PQR onto triangle P11Q11R11
Date posted:
May 9, 2019
.
Answers (1)
-
In the figure below, AB is a diameter of the circle. Chord PQ intersects AB at N. BR which is a tangent to the circle...
(Solved)
In the figure below, AB is a diameter of the circle. Chord PQ intersects AB at N. BR which is a tangent to the circle at B
meets PQ produced at R.
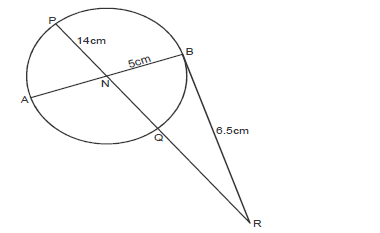
Given that PN = 14cm, NB = 5cm and BR = 6.5cm.
Calculate :
a) NR
b) AN
Date posted:
May 9, 2019
.
Answers (1)
-
PQRS is a trapezium where PQ is parallel to SR. PR and SQ intersect at X, so that SX = kSQ and PX = hPR...
(Solved)
PQRS is a trapezium where PQ is parallel to SR. PR and SQ intersect at X, so that SX = kSQ and PX = hPR where k and h
are constants.
Vectors PQ = 3q and PS = s, SR = q
a) Show this information on a diagram.
b) Express vector SQ in terms of s and q
c) Express SX in terms of k, q and s
d) Express SX in terms of h, q and s
e) Obtain h and k
f) In what ratio does X divide SQ ?
Date posted:
May 9, 2019
.
Answers (1)
-
A certain number of people agreed to contribute equally to buy books worth shs.1200 for a school library. Five people
pulled out and so that others...
(Solved)
A certain number of people agreed to contribute equally to buy books worth shs.1200 for a school library. Five people
pulled out and so that others agreed to contribute an extra sh.40 each. Their contribution enabled them to raise the
sh.1200 expected.
a) If the original number of people was x, write an expression of how much each was originally going to contribute.
b) Write down the expression of how much each contributed after the five people pulled out.
c) Calculate how many people made the contribution.
d) If the prices of books before buying went up in the ratio 5 : 4 how much extra did each contributor give.
Date posted:
May 9, 2019
.
Answers (1)
-
Three ships P, Q and R are at sea such that ship Q is 400km on a bearing of 030o from ship P. Ship R...
(Solved)
Three ships P, Q and R are at sea such that ship Q is 400km on a bearing of 030o from ship P. Ship R is 750km from
ship Q and on a bearing of S60oE from ship Q. Ship Q is 1000km and to the north of an enemy ship S.
a) Taking a scale of 1cm to represent 100km, locate the position of ships P, Q, R and S.
b) Find the compass bearing of :
i) ship P from ship S
ii) ship S from ship R
c) Use the scale drawing to determine
i) the distance of S from P
ii) the distance of R from S
d) Find the bearing of :
i) Q from R
ii) P from R
Date posted:
May 9, 2019
.
Answers (1)
-
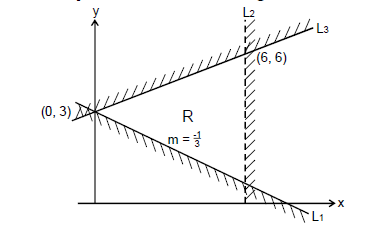
Write down the three inequalities which define the region R.
(Solved)
Write down the three inequalities which define the region R.
Date posted:
May 9, 2019
.
Answers (1)
-
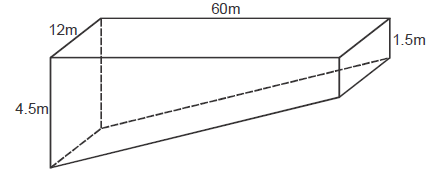
The figure below represents a swimming pool. Calculate the volume of the swimming pool in litres.
(Solved)
The figure below represents a swimming pool. Calculate the volume of the swimming pool in litres.
Date posted:
May 9, 2019
.
Answers (1)
-
The first, the 7th and the 25th terms of an arithmetic progression are the first three consecutive terms of a geometrical progression. The 20th term...
(Solved)
The first, the 7th and the 25th terms of an arithmetic progression are the first three consecutive terms of a geometrical progression. The 20th term of the arithmetic progression is 22. Find:
a) i) The first term and common difference of the arithmetic progression.
ii) The sum of the first 40 terms of the arithmetic progression.
b) i) The 10th term of the geometric progression.
ii) The sum of the first 10 terms of the geometric progression.
Date posted:
May 9, 2019
.
Answers (1)
-
Find the percentage error in calculating the volume of the cuboid whose dimensions are 8.2cm by 6.2cm by 5.7cm
(Solved)
Find the percentage error in calculating the volume of the cuboid whose dimensions are 8.2cm by 6.2cm by 5.7cm
Date posted:
May 9, 2019
.
Answers (1)
-
OA = 2i + 3j + 4k while OB = 5i + 9j - 2k. P divides AP externally in the ratio 2 : 1....
(Solved)
OA = 2i + 3j + 4k while OB = 5i + 9j - 2k. P divides AP externally in the ratio 2 : 1. Find he coordinates of P.
Date posted:
May 9, 2019
.
Answers (1)
-
Find the value of k if 4x² + 25x + 5 + k is a perfect square.
(Solved)
Find the value of k if 4x² + 25x + 5 + k is a perfect square.
Date posted:
May 9, 2019
.
Answers (1)
-
Using mid-ordinate rule of 5 strips, determine the area under the curve y = 3x² + 10, the lines x = 1, x=6 and x-axis.
(Solved)
Using mid-ordinate rule of 5 strips, determine the area under the curve y = 3x² + 10, the lines x = 1, x=6 and x-axis.
Date posted:
May 9, 2019
.
Answers (1)
-
A bus left Nairobi at 7.00 am and travelled towards Eldoret at an average speed of 80km/hr. At 7.45am a car left
Eldoret towards Nairobi at...
(Solved)
A bus left Nairobi at 7.00 am and travelled towards Eldoret at an average speed of 80km/hr. At 7.45am a car left
Eldoret towards Nairobi at an average speed of 120km/hr. The distance between Nairobi and Eldoret is 300km.
Calculate
a) the time the bus arrived at Eldoret.
b) the time of the day the two met
c) the distance from Nairobi where the two met.
d) the distance of the bus from Eldoret when the car arrived at Nairobi.
Date posted:
May 9, 2019
.
Answers (1)
-
A boat at point X is 200m to the south of point Y. The boat sails from X to another point Z. Point Z is...
(Solved)
A boat at point X is 200m to the south of point Y. The boat sails from X to another point Z. Point Z is 200m on a
bearing of 310° from X. Point X, Y and Z are on the same horizontal plane.
a) Calculate the bearing and distance of Z from Y.
b) W is the point on the path of the boat nearest to point Y. Calculate the distance WY.
c) A vertical tower stands at point Y. The angle of depression of point x from the top of the tower is 6°. Calculate the
angle of elevation of the top of the tower from point W.
Date posted:
May 8, 2019
.
Answers (1)
-
The table below shows the distribution of marks scored by 100 candidates in an examination.
(Solved)
The table below shows the distribution of marks scored by 100 candidates in an examination.

a) Find k.
b) Using an assumed mean of 44.5 calculate.
i) The mean
ii) The standard deviation.
c) Calculate the median
Date posted:
May 8, 2019
.
Answers (1)
-
A flower garden is in the form of the trapezium shown below. Find the area of the garden in m²
(Solved)
A flower garden is in the form of the trapezium shown below. Find the area of the garden in m²

Date posted:
May 8, 2019
.
Answers (1)
-
Half of the interior angles of an irregular hexagon are in the ratio 2 : 3 : 4, while the other half are in the...
(Solved)
Half of the interior angles of an irregular hexagon are in the ratio 2 : 3 : 4, while the other half are in the ratio 4 : 3 : 5 .
List the interior angles of the hexagon.
Date posted:
May 8, 2019
.
Answers (1)
-
When a certain number is divided by 30, 45 or 54, there is always a remainder of 21. Find the least number
(Solved)
When a certain number is divided by 30, 45 or 54, there is always a remainder of 21. Find the least number
Date posted:
May 8, 2019
.
Answers (1)
-
A particle moving with acceleration a = (10 –t) m/s2. When t = 1 velocity V = 2 m/s and when t = 0 displacement...
(Solved)
A particle moving with acceleration a = (10 –t) m/s2. When t = 1 velocity V = 2 m/s and when t = 0 displacement S =
OM.
(a) Express displacement and velocity in terms of t.
(b) Calculate the velocity when t = 35
(c) What is the displacement when t = 5
(d) Calculate maximum velocity.
Date posted:
May 8, 2019
.
Answers (1)
-
Find the coordinates of the image of a point (5, -3) when its rotated through 1800 about (3,1).
(Solved)
Find the coordinates of the image of a point (5, -3) when its rotated through 1800 about (3,1).
Date posted:
May 8, 2019
.
Answers (1)