- A line L is perpendicular to 3y - 4x = 7. Determine the acute angle between L and the x-axis.(Solved)
A line L is perpendicular to 3y - 4x = 7. Determine the acute angle between L and the x-axis.
Date posted: May 9, 2019. Answers (1)
- Evaluate without using tables or a calculator.(Solved)
Evaluate without using tables or a calculator.
100-1.5 X 320.2
Date posted: May 9, 2019. Answers (1)
- a) Complete the table below for the values of sin 2x and 2 cos (x - 30o)(Solved)
a) Complete the table below for the values of sin 2x and 2 cos (x - 30o)

b) On the grid provided, use a suitable scale to draw the graphs of y = sin 2x and y = 2 cos (x - 30o)
for 0o ≤ x ≤ 180o
c) Using the graph in part (b) above.
i) Estimate the solution to the equation 2cos (x - 30o) - sin 2x = 0 for 0o ≤ x ≤ 180o
ii) Estimate the value of x for which 4 cos (x - 30o) + 3 = 0
Date posted: May 9, 2019. Answers (1)
- The table below shows marks scored by 40 candidates in an examination.(Solved)
The table below shows marks scored by 40 candidates in an examination.
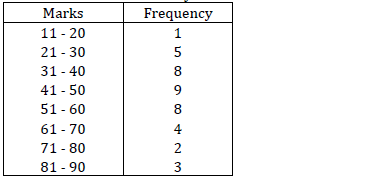
a) Using an assumed mean of 45.5 estimate :
i) Mean
ii) Standard deviation
b) Calculate the quartile deviation.
Date posted: May 9, 2019. Answers (1)
- The sketch below shows curve y = 2x2 + 4x + 3 and a straight line intersecting the curve at points A and B.(Solved)
The sketch below shows curve y = 2x2 + 4x + 3 and a straight line intersecting the curve at points A and B.
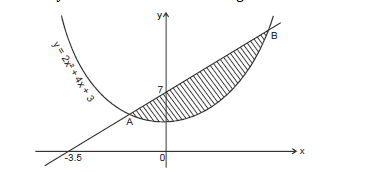
If the x-intercepts is -3.5 and the y-intercept is 7, find :
a) the equation of the straight line.
b) the coordinates of A and B
c) the area of the shaded region
Date posted: May 9, 2019. Answers (1)
- In the figure below, ABCDEF is a wedge. BC = 6cm, DC = 8cm and ED = 15cm.(Solved)
In the figure below, ABCDEF is a wedge. BC = 6cm, DC = 8cm and ED = 15cm.
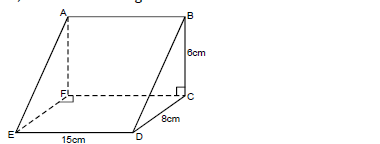
Find the :
a) length BE
b) angle between BE and the plane EDCF
c) angle between plane ABDE and the plane EDCF
d) volume of the wedge
Date posted: May 9, 2019. Answers (1)
- Mrs Mureithi has 20 acres of land. She intends to grow maize and beans. She requires sh.2000 to plant an acre of maize
and sh.4000 for...(Solved)
Mrs Mureithi has 20 acres of land. She intends to grow maize and beans. She requires sh.2000 to plant an acre of maize
and sh.4000 for an acre of beans. Twice the area to be planted with maize should not be less than one of beans. The
total capital available is sh.60000. The estimated profit is sh.5000 for an acre of maize and sh.7000 for an acre of
beans.
By letting x and y to represent the area to be planted with maize and beans respectively.
a) Find the inequalities to represent the information.
b) On the grid provided, represent the inequalities and show the region which satisfy the condition.
c) Determine the expected maximum profit.
Date posted: May 9, 2019. Answers (1)
- a) MNQR is a rectangle in which MN = 5cm and NQ = 8cm. Construct the locus of a point P within the rectangle
which is...(Solved)
a) MNQR is a rectangle in which MN = 5cm and NQ = 8cm. Construct the locus of a point P within the rectangle
which is such that P is equidistant from sides NM and NQ
c) The locus of P in (a) above cuts MR at T. Draw a circle whose centre O is equidistant from the three sides of
triangle MNT and its radius is OM
c) In rectangle MNQR above, construct the locus of a variable point V such that 40o ≤ QVR ≤ 90o
Date posted: May 9, 2019. Answers (1)
- A triangle PQR whose vertices are P(2, 2), Q(5, 3) and R(4, 1) is mapped onto triangle P1Q1R1 by a transformation
whose matrix is(Solved)
A triangle PQR whose vertices are P(2, 2), Q(5, 3) and R(4, 1) is mapped onto triangle P1Q1R1 by a transformation
whose matrix is

a) On the grid provided below, draw triangle PQR and triangle P1Q1R1
b) Triangle P1Q1R1 is mapped onto a triangle whose vertices are P11(-2, -2), Q11(-5, -3) and R11(-4, -1)
i) Draw triangle P11Q11R11 on the same grid.
ii) Find the matrix representing transformation that maps triangle P1Q1R1 onto triangle P11Q11R11
c) Describe the transformation that maps PQR onto triangle P11Q11R11
Date posted: May 9, 2019. Answers (1)
- In 2001 the salaries of Gitonga and Cherop were sh.252000 per annum and sh.216000 per annum respectively. Their
employers decided to increase their salaries as follows.
Gitonga’s...(Solved)
In 2001 the salaries of Gitonga and Cherop were sh.252000 per annum and sh.216000 per annum respectively. Their
employers decided to increase their salaries as follows.
Gitonga’s employer decided to give him fixed annual increments throughout his employment period, with first
increment in January 2002.Cherop’s employer decided to give her increments of 8% compounded annually throughout her employment period with the first increment in January 2002.
a) If Gitonga annual salary in 2009 was sh.346080, calculate his annual increment.
b) How much money in total did Gitonga earn from is salaries from 1st January 2001 to 31st December 2009 ?
c) Determine Cherop’s monthly salary of August 2009.
d) How much money in total did Cherop earn from her salaries from 1st January 2001 to 31st December 2009.
e) Determine the difference between Gitonga’s and Cherop’s average yearly earnings from 1st January 2001 to 31st
December 2009.
Date posted: May 9, 2019. Answers (1)
- In the figure below, AB is a diameter of the circle. Chord PQ intersects AB at N. BR which is a tangent to the circle...(Solved)
In the figure below, AB is a diameter of the circle. Chord PQ intersects AB at N. BR which is a tangent to the circle at B
meets PQ produced at R.
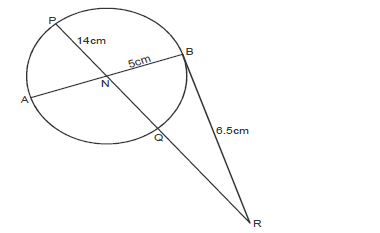
Given that PN = 14cm, NB = 5cm and BR = 6.5cm.
Calculate :
a) NR
b) AN
Date posted: May 9, 2019. Answers (1)
- Given OX = 4i + j + 3k and OY = 7i - 5j + k. If M is the mid-point of line XY, determine...(Solved)
Given OX = 4i + j + 3k and OY = 7i - 5j + k. If M is the mid-point of line XY, determine the modulus of XM.
Date posted: May 9, 2019. Answers (1)
- The table below is part of the tax table for monthly income for the year 2007.(Solved)
The table below is part of the tax table for monthly income for the year 2007.
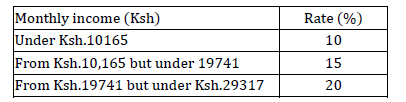
In that year, Adan’s monthly gross tax was Ksh.2,885. Calculate his monthly income.
Date posted: May 9, 2019. Answers (1)
- An aeroplane took off from an airport at (68oN, 86oE) and flew due West for a distance of 1000 nautical miles before landing. Find to...(Solved)
An aeroplane took off from an airport at (68oN, 86oE) and flew due West for a distance of 1000 nautical miles before landing. Find to the nearest degree, the coordinates of the place where the plane landed.
Date posted: May 9, 2019. Answers (1)
- Two students are selected at random from a class of 15 boys and 10 girls. Find the probability that(Solved)
Two students are selected at random from a class of 15 boys and 10 girls. Find the probability that
a) they are both boys
b) one is a boy and the other is a girl
Date posted: May 9, 2019. Answers (1)
- Simplify leaving your answer in surd form(Solved)
Simplify leaving your answer in surd form
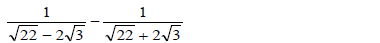
Date posted: May 9, 2019. Answers (1)
- a) Complete the following table for the function y = 6 + 3x - 2x2(Solved)
a) Complete the following table for the function y = 6 + 3x - 2x2

b) Using the completed table and the trapezoidal rule with 10 strips, estimate the area bounded by the curve and the
lines y = -8 and x = -1.5
Date posted: May 9, 2019. Answers (1)
- The coordinates of the ends of a diameter of a circle are (6, 4) and (-2, 2). If the centre of the circle is Q,...(Solved)
The coordinates of the ends of a diameter of a circle are (6, 4) and (-2, 2). If the centre of the circle is Q, determine:
a) the coordinates of centre Q
b) the equation of the circle expressing it in the form x2 + y2 + ax + by + c = 0 where a, b and c are constants.
Date posted: May 9, 2019. Answers (1)
- The length and width of a rectangle measured to the nearest centimetre are 10cm and 6cm respectively. Calculate the
percentage error in the area giving your...(Solved)
The length and width of a rectangle measured to the nearest centimetre are 10cm and 6cm respectively. Calculate the
percentage error in the area giving your answer to 1 decimal place.
Date posted: May 9, 2019. Answers (1)
- Solve for x,given that;(Solved)
Solve for x,given that;

Date posted: May 9, 2019. Answers (1)