- Define the Taylor’s Series from Laurent Series(Solved)
Define the Taylor’s Series from Laurent Series
Date posted: May 10, 2019. Answers (1)
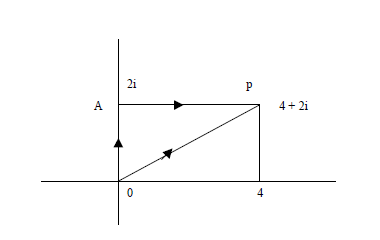
- a) Integrate z2 along the straight line OM (direct) and also along the path OLM
consisting of two straight line segments OL and LM. O is...(Solved)
a) Integrate z2 along the straight line OM (direct) and also along the path OLM
consisting of two straight line segments OL and LM. O is the origin and M is the
point z = 3 + i.
b) Show that the integral of z2 along the two different paths are equal.
c) Is the result true for any function other than z2 for the two paths?
Date posted: May 10, 2019. Answers (1)
- Evaluate the following expression(Solved)
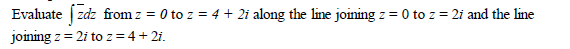
Date posted: May 10, 2019. Answers (1)
- a)Evaluate the following expression where c is any simple closed curve c and a is inside c,(Solved)
a)Evaluate the following expression where c is any simple closed curve c and a is inside c,

b) What is the value of the integral if a is outside the closed curve?
Date posted: May 10, 2019. Answers (1)
- If f(z) is analytic inside and on the boundary c of a simply connected region R and a is
any point inside the curve c then,(Solved)
If f(z) is analytic inside and on the boundary c of a simply connected region R and a is
any point inside the curve c then,

Prove
Date posted: May 10, 2019. Answers (1)
- Find the fixed points of the bilinear transformation(Solved)
Find the fixed points of the bilinear transformation

Date posted: May 10, 2019. Answers (1)
- Find the fixed points of the bilinear transformation(Solved)
Find the fixed points of the bilinear transformation

Date posted: May 10, 2019. Answers (1)
- a) Find a bilinear transformation, which transforms the unit circle |z| = 1 into the real
axis of the w plane in such a way that...(Solved)
a) Find a bilinear transformation, which transforms the unit circle |z| = 1 into the real
axis of the w plane in such a way that the points z1 = 1, z2 = i, z3 = -1 are mapped onto w1 = 0, w2 = 1, w3 = infinite.
b) In what regions the interior and exterior of the circle are mapped.
Date posted: May 10, 2019. Answers (1)
- Find a bilinear transformation which maps the points(Solved)
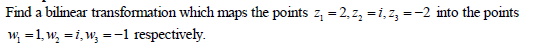
Date posted: May 10, 2019. Answers (1)
- Find a bilinear transformation which maps the point z = 0, -i, -1 on the z plane into
w = i, 1, 0 respectively on the...(Solved)
Find a bilinear transformation which maps the point z = 0, -i, -1 on the z plane into
w = i, 1, 0 respectively on the w plane.
Date posted: May 10, 2019. Answers (1)
- Explain the nature of the transformation w = z2 considering the semi-circle with centre
the origin and the radius r on the z –plane(Solved)
Explain the nature of the transformation w = z2 considering the semi-circle with centre
the origin and the radius r on the z –plane.
Date posted: May 10, 2019. Answers (1)
- Let w = 3z + 4 – 5i = f(z)
Find the values of w which corresponds to z = -3 + i on the z...(Solved)
Let w = 3z + 4 – 5i = f(z)
Find the values of w which corresponds to z = -3 + i on the z plane.
Date posted: May 10, 2019. Answers (1)
- Find the image of the point (4, 3) on z plane under the transformation w = 2z2 + 3.(Solved)
Find the image of the point (4, 3) on z plane under the transformation w = 2z2 + 3.
Date posted: May 10, 2019. Answers (1)
- Prove that sin z = sin x cos hy + i cos x sin hy(Solved)
Prove that sin z = sin x cos hy + i cos x sin hy
Date posted: May 10, 2019. Answers (1)
- Find all values of z such that(Solved)
Find all values of z such that

Date posted: May 10, 2019. Answers (1)
- Find all values of z such that ez = 2(Solved)
Find all values of z such that ez = 2
Date posted: May 10, 2019. Answers (1)
- Show that(Solved)
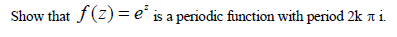
Date posted: May 10, 2019. Answers (1)
- Prove that(Solved)
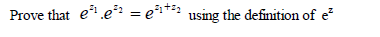
Date posted: May 10, 2019. Answers (1)
- Show that the function;(Solved)
Show that the function;

is not analytic at the origin, although the Cauchy –Reimann equations are satisfied at the origin.
Date posted: May 10, 2019. Answers (1)
- Let f (z) = u(x, y) + iv(x, y) .Prove that(Solved)
Let f (z) = u(x, y) + iv(x, y) .Prove that
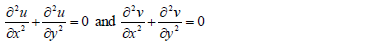
Date posted: May 10, 2019. Answers (1)