- Expand the function below(Solved)
Expand the function below

Date posted: May 10, 2019. Answers (1)
- Expand the following function(Solved)
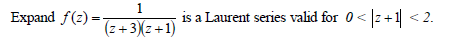
Date posted: May 10, 2019. Answers (1)
- Expand the function below in a Laurent Series at z = 3.(Solved)
Expand the function below in a Laurent Series at z = 3.

Date posted: May 10, 2019. Answers (1)
- Consider the function(Solved)
Consider the function

a) state the singularity of f(z)
b) what is the kind of singularity of f(z).
c) expand f(z) in a Laurent series.
d) state the region of convergence of the series.
Date posted: May 10, 2019. Answers (1)
- Consider the function below. a) state the singularity of f(z). b) what is the kind of singularity of f(z).(Solved)
Consider the function

a) state the singularity of f(z).
b) what is the kind of singularity of f(z).
c) find the Laurent series of f(z).
d) what is the region of convergence of f(z)?.
Date posted: May 10, 2019. Answers (1)
- Consider the function a) state the singularity of f(z). b) what is the kind of the singularity of f(z).(Solved)
Consider the function

a) state the singularity of f(z).
b) what is the kind of the singularity of f(z).
c) expand f(z) in a Laurent series.
d) state the region of convergence of the series.
Date posted: May 10, 2019. Answers (1)
- Show that the function below has an essential singularity at z = 3.(Solved)
Show that the function below has an essential singularity at z = 3.

Date posted: May 10, 2019. Answers (1)
- Define a Pole(Solved)
Define a Pole
Date posted: May 10, 2019. Answers (1)
- Define Isolated Singular points.(Solved)
Define Isolated Singular points.
Date posted: May 10, 2019. Answers (1)
- Define the Taylor’s Series from Laurent Series(Solved)
Define the Taylor’s Series from Laurent Series
Date posted: May 10, 2019. Answers (1)
- a) Integrate z2 along the straight line OM (direct) and also along the path OLM
consisting of two straight line segments OL and LM. O is...(Solved)
a) Integrate z2 along the straight line OM (direct) and also along the path OLM
consisting of two straight line segments OL and LM. O is the origin and M is the
point z = 3 + i.
b) Show that the integral of z2 along the two different paths are equal.
c) Is the result true for any function other than z2 for the two paths?
Date posted: May 10, 2019. Answers (1)
- Evaluate the following expression(Solved)
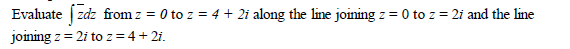
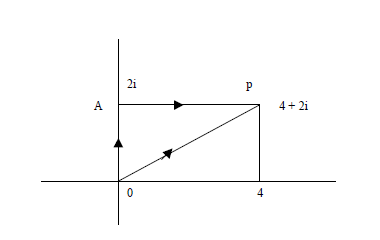
Date posted: May 10, 2019. Answers (1)
- a)Evaluate the following expression where c is any simple closed curve c and a is inside c,(Solved)
a)Evaluate the following expression where c is any simple closed curve c and a is inside c,

b) What is the value of the integral if a is outside the closed curve?
Date posted: May 10, 2019. Answers (1)
- If f(z) is analytic inside and on the boundary c of a simply connected region R and a is
any point inside the curve c then,(Solved)
If f(z) is analytic inside and on the boundary c of a simply connected region R and a is
any point inside the curve c then,

Prove
Date posted: May 10, 2019. Answers (1)
- Find the fixed points of the bilinear transformation(Solved)
Find the fixed points of the bilinear transformation

Date posted: May 10, 2019. Answers (1)
- Find the fixed points of the bilinear transformation(Solved)
Find the fixed points of the bilinear transformation

Date posted: May 10, 2019. Answers (1)
- a) Find a bilinear transformation, which transforms the unit circle |z| = 1 into the real
axis of the w plane in such a way that...(Solved)
a) Find a bilinear transformation, which transforms the unit circle |z| = 1 into the real
axis of the w plane in such a way that the points z1 = 1, z2 = i, z3 = -1 are mapped onto w1 = 0, w2 = 1, w3 = infinite.
b) In what regions the interior and exterior of the circle are mapped.
Date posted: May 10, 2019. Answers (1)
- Find a bilinear transformation which maps the points(Solved)
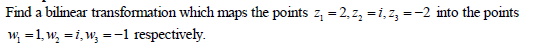
Date posted: May 10, 2019. Answers (1)
- Find a bilinear transformation which maps the point z = 0, -i, -1 on the z plane into
w = i, 1, 0 respectively on the...(Solved)
Find a bilinear transformation which maps the point z = 0, -i, -1 on the z plane into
w = i, 1, 0 respectively on the w plane.
Date posted: May 10, 2019. Answers (1)
- Explain the nature of the transformation w = z2 considering the semi-circle with centre
the origin and the radius r on the z –plane(Solved)
Explain the nature of the transformation w = z2 considering the semi-circle with centre
the origin and the radius r on the z –plane.
Date posted: May 10, 2019. Answers (1)