- Prove that(Solved)
Prove that

Date posted: May 10, 2019. Answers (1)
- Evaluate the following function(Solved)
Evaluate the following function

Date posted: May 10, 2019. Answers (1)
- Evaluate the expression given below(Solved)
Evaluate the expression given below

when
i). c is the circle |z| = 5
ii). c is the circle |z| = 3
iii). c is the circle |z| = 1
Date posted: May 10, 2019. Answers (1)
- Evaluate the expression below(Solved)
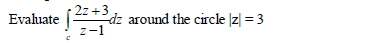
Date posted: May 10, 2019. Answers (1)
- Prove the Residue Theorem(Solved)
Prove the Residue Theorem
Date posted: May 10, 2019. Answers (1)
- Determine the pole of f(z). Calculate the residue of f(z) at its poles.(Solved)
Determine the pole of f(z). Calculate the residue of f(z) at its poles.

Date posted: May 10, 2019. Answers (1)
- a) Determine the pole of f(z)(Solved)
a) Determine the pole of f(z)

b) Calculate the residue of f(z) at its pole.
Date posted: May 10, 2019. Answers (1)
- Find the poles of(Solved)
Find the poles of

Date posted: May 10, 2019. Answers (1)
- Determine the poles of(Solved)
Determine the poles of

Date posted: May 10, 2019. Answers (1)
- Find the poles of the function given below and state the order of each pole.(Solved)
Find the poles of the function given below and state the order of each pole.

Date posted: May 10, 2019. Answers (1)
- Expand the function below(Solved)
Expand the function below

Date posted: May 10, 2019. Answers (1)
- Expand the following function(Solved)
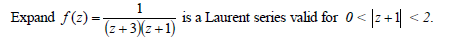
Date posted: May 10, 2019. Answers (1)
- Expand the function below in a Laurent Series at z = 3.(Solved)
Expand the function below in a Laurent Series at z = 3.

Date posted: May 10, 2019. Answers (1)
- Consider the function(Solved)
Consider the function

a) state the singularity of f(z)
b) what is the kind of singularity of f(z).
c) expand f(z) in a Laurent series.
d) state the region of convergence of the series.
Date posted: May 10, 2019. Answers (1)
- Consider the function below. a) state the singularity of f(z). b) what is the kind of singularity of f(z).(Solved)
Consider the function

a) state the singularity of f(z).
b) what is the kind of singularity of f(z).
c) find the Laurent series of f(z).
d) what is the region of convergence of f(z)?.
Date posted: May 10, 2019. Answers (1)
- Consider the function a) state the singularity of f(z). b) what is the kind of the singularity of f(z).(Solved)
Consider the function

a) state the singularity of f(z).
b) what is the kind of the singularity of f(z).
c) expand f(z) in a Laurent series.
d) state the region of convergence of the series.
Date posted: May 10, 2019. Answers (1)
- Show that the function below has an essential singularity at z = 3.(Solved)
Show that the function below has an essential singularity at z = 3.

Date posted: May 10, 2019. Answers (1)
- Define a Pole(Solved)
Define a Pole
Date posted: May 10, 2019. Answers (1)
- Define Isolated Singular points.(Solved)
Define Isolated Singular points.
Date posted: May 10, 2019. Answers (1)
- Define the Taylor’s Series from Laurent Series(Solved)
Define the Taylor’s Series from Laurent Series
Date posted: May 10, 2019. Answers (1)