- a) Fill in the table below.(Solved)
a) Fill in the table below.
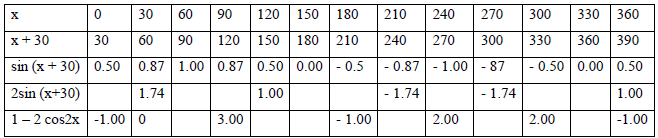
b) On the same axes sketch the following curves;
y = 2 sin(x + 30) and y = 1 –2 cos 2x.
(c) Use your graph to solve the equation
2 sin (x + 30) + cos 2x = 1
(d) Find the;
(i) Period of y = 1 – cos2x
(ii) Phase angle of y = 2 sin (x + 30°)
Date posted: August 19, 2019. Answers (1)
- The graph below gives the motion of a car for some distance. Determine the total distance traveled.(Solved)
The graph below gives the motion of a car for some distance. Determine the total distance traveled.
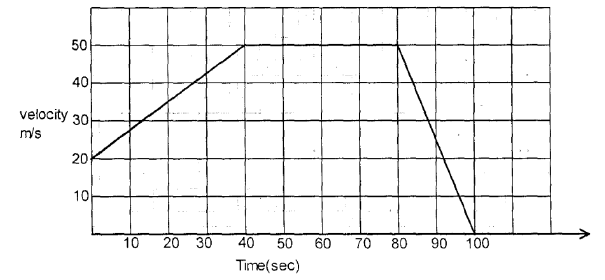
Date posted: August 19, 2019. Answers (1)
- Solve the following pair of inequalities and represent the solution on the number line.(Solved)
Solve the following pair of inequalities and represent the solution on the number line.

Date posted: August 19, 2019. Answers (1)
- Two quantities P and n, are connected by the equation P = AKn, where A and K are constants. The table below shows some corresponding...(Solved)
Two quantities P and n, are connected by the equation P = AKn, where A and K are constants. The table below shows some corresponding values of n and P.

(a) State the linear equation connecting P and n.
(b) On the grid provided, draw a suitable straight line.
(c) Use your graph to estimate the value A and k.
Date posted: August 19, 2019. Answers (1)
- Find the acute angle y if sin 4y = cos 2y.(Solved)
Find the acute angle y if sin 4y = cos 2y.
Date posted: August 19, 2019. Answers (1)
- Solve for x and y in the following equations(Solved)
Solve for x and y in the following equations
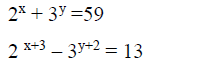
Date posted: August 19, 2019. Answers (1)
- The field book below gives measurements of a field. The distances are given in metres and AF = 100 m.(Solved)
The field book below gives measurements of a field. The distances are given in metres and AF = 100 m.
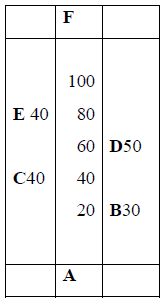
(a) Using a scale of 1cm represents 10m, draw a map of the field with straight boundary edges.
(b)
(i) Find the area of the field in square metres.
(ii) Determine the area of the field in hectares.
Date posted: August 19, 2019. Answers (1)
- A particle moves along a straight line such that its displacement S metres from a given point is(Solved)
A particle moves along a straight line such that its displacement S metres from a given point is
S = t3 – 5t2 + 3t + 4 where t is time in seconds.
Find:
(a) The displacement of the particle at t = 5
(b) The velocity of the particle when t = 5
(c) The values of t when the particle is momentarily at rest.
(d) The acceleration of the particle when t = 2.
Date posted: August 19, 2019. Answers (1)
- The frequency distribution table below shows lengths in cm for 41 pieces(Solved)
The frequency distribution table below shows lengths in cm for 41 pieces
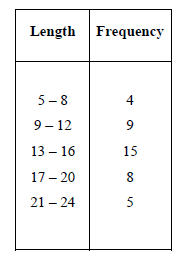
Calculate the:
(a) Mean.
(b) Median
(c) Standard deviation
Date posted: August 19, 2019. Answers (1)
- Mr. Omwega is employed. His basic salary is Kshs. 21, 750 and is entitled(Solved)
Mr. Omwega is employed. His basic salary is Kshs. 21, 750 and is entitled to a house allowance of
Kshs 15, 000 and a travelling allowance of Kshs 8, 000 per month. He also claims a family monthly relief of Kshs 1, 056 per month. Other deductions are; Union dues Kshs 200 and Co-operative shares Kshs 4, 500 per month.
The table below shows the tax rates for the year.

Calculate;
(a) Mr. Omwega’s annual taxable income.
(b) The tax paid by Mr. Omwega in the year.
(c) Mr. Omwega’s net income per month
Date posted: August 19, 2019. Answers (1)
- A fritter bought 144 pineapples atsh100 for every six pineapples. She sold them of at sh72 for every three and rest at sh60 for every...(Solved)
A fritter bought 144 pineapples atsh100 for every six pineapples. She sold them of at sh72 for every three and rest at sh60 for every two.if she made 65% profit. Calculate the number of pineapples sold at sh72 for every three.
Date posted: August 18, 2019. Answers (1)
- Triangle ABC has co-ordinates A(2,7) B (2,2) and C (7,-2) .The triangle is reflected in the y-axis followed by a reflection in the line x=2,...(Solved)
Triangle ABC has co-ordinates A(2,7) B (2,2) and C (7,-2) .The triangle is reflected in the y-axis followed by a reflection in the line x=2, without drawing determine the co-ordinates of the final image
Date posted: August 16, 2019. Answers (1)
- A madline is valued at Ksh. 100,000. If the rate of depreciation is 0.9% per month .Calculate the time it takes for the value to...(Solved)
A madline is valued at Ksh. 100,000. If the rate of depreciation is 0.9% per month .Calculate the time it takes for the value to drop to Ksh .50, 000.
Date posted: August 16, 2019. Answers (1)
- Mary is four times as old as her last born John. In seven years time, the sum of their ages will be 59 years. Determine...(Solved)
Mary is four times as old as her last born John. In seven years time, the sum of their ages will be 59 years. Determine their ages three years ago.
Date posted: August 16, 2019. Answers (1)
- In the figure below ABX is a tangent to the circle at B . Angle CAB = 17o and < ACB = 36o.Calculate < CBX.
(Solved)
In the figure below ABX is a tangent to the circle at B . Angle CAB = 17o and < ACB = 36o.Calculate < CBX.
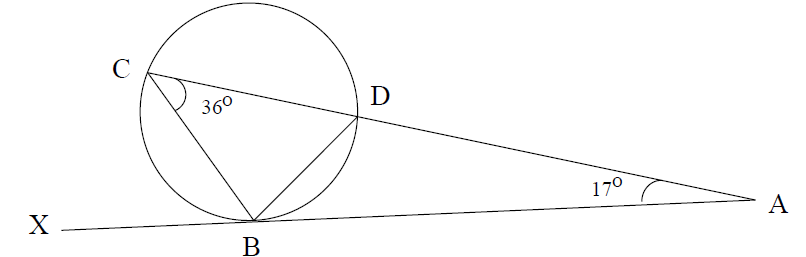
Date posted: August 16, 2019. Answers (1)
- Find the value of x in the following equation
25x-1 + 52x = 130(Solved)
Find the value of x in the following equation
25x-1 + 52x = 130
Date posted: August 16, 2019. Answers (1)
- Solve the inequality -3x + 2(Solved)
Solve the inequality -3x + 2
Date posted: August 16, 2019. Answers (1)
- The gradient of a line L through points A (2x, 4) and B (-1, X) is 1/7.Find the equation of a line perpendicular to L...(Solved)
The gradient of a line L through points A (2x, 4) and B (-1, X) is 1/7.Find the equation of a line perpendicular to L through B
Date posted: August 16, 2019. Answers (1)
- Without using a calculator , evaluate.(Solved)
Without using a calculator , evaluate.

Date posted: August 16, 2019. Answers (1)
- A particle travels in a straight line through a fixed point O such that its displacement S metres, from O is given by S =...(Solved)
A particle travels in a straight line through a fixed point O such that its displacement S metres, from O is given by S = 3t3 – 27t2 + 72t + 4 where t is the time in seconds after passing O.
Calculate;
a) The displacement of the particle at t = 3.
b) The value of t for which the particle is momentarily at rest.
c) The acceleration when t = 4.
d) At what time is its minimum velocity?
Date posted: August 16, 2019. Answers (1)