- Solve for x in the equation log8 (x + 5) – log8 (x – 3) = 2/3(Solved)
Solve for x in the equation log8 (x + 5) – log8 (x – 3) = 2/3
Date posted: September 11, 2019. Answers (1)
- Make b the subject of the formula.(Solved)
Make b the subject of the formula.
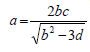
Date posted: September 11, 2019. Answers (1)
- Use logarithms to evaluate correct to 4 s.f(Solved)
Use logarithms to evaluate correct to 4 s.f
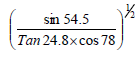
Date posted: September 11, 2019. Answers (1)
- The product of the first three terms of geometric progression is 729.(Solved)
The product of the first three terms of geometric progression is 729. If the first term is a and the common ratio is r.
(a) Express r in terms of a.
(b) Given the sum of the three terms is 39.
(i) Find the values of a and r and hence write down two possible sequences each up to the 4th term.
(ii) Find the product of the 10th term of the two sequences.
Date posted: September 11, 2019. Answers (1)
- The diagram below shows triangle ABC, such that CA = 2a and CB = 3b.(Solved)
The diagram below shows triangle ABC, such that CA = 2a and CB = 3b. M is the midpoint of CA. N is a point on AB such that 2 AN = NB and R is a point on AB produced such that 2 AR = 5RB. If K is the point of intersection of MR and CN,
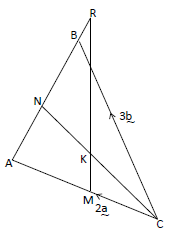
(a) Express in terms of a and b.
(i) AB.
(ii) CN.
(iii) BR.
(iv) MR.
(v) CK.
(b) Find the ratio CK: KN.
Date posted: September 11, 2019. Answers (1)
- Two quantities P and r are connected by the equation P = Krn. Where k and n are constants.The table of values of P and...(Solved)
Two quantities P and r are connected by the equation P = Krⁿ. Where k and n are constants.The table of values of P and r is given below.
(a) State the linear equation connecting P and r.
(b) (i) Using a suitable scale, draw a suitable line graph from the above data on the grid provided.
(ii) Using your graph, estimate the values of K and n.
(c) Find the relation connecting P and r.
Date posted: September 11, 2019. Answers (1)
- The table below shows the distribution of marks scored by 50 students of Afraha high.(Solved)
The table below shows the distribution of marks scored by 50 students of Afraha high.
Calculate:-
(a) interquartile range.
(b) Mean mark
(c) Standard deviation
Date posted: September 11, 2019. Answers (1)
- Every morning during class time, Brenda either reads a novel or solves Mathematics questions. The
probability that she reads a novel is 4/5. (Solved)
Every morning during class time, Brenda either reads a novel or solves Mathematics questions. The probability that she reads a novel is 4/5. If she reads a novel, there is a probability of 3/7 that she will fall asleep. If she solves Math’s questions there is a probability of 1/2 that she will fall asleep. Sometimes the teacher on duty enters Brenda’s classroom. When Brenda is asked whether she had been a sleep, there is a probability of 1/5 that she will admit that she had been asleep and a probability of 3/5 that she will claim to have been asleep.
Using a tree diagram;
Find the probability that
(i) She sleeps and admits it.
(ii) She sleeps and does not admit.
(iii) She does not sheep but claims to have been asleep.
(iv) She does not sleep and says that she has not been a slept.
(v) She sleeps and admits and changes her mind.
Date posted: September 11, 2019. Answers (1)
- (a) Fill the table below using the following function y = 3 + 4x - 2x²(Solved)
(a) Fill the table below using the following function y = 3 + 4x - 2x²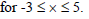 
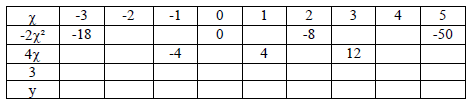
(b) On the grid provided, draw the graph of the function y = 3 + 4x - 2x²
(c) Using your graph; estimate the roots of the equations:-
(i) 3 + 4x = 2x².
(ii) 2x²- 3x - 6 = 0.
(d) State the y – co-ordinate of the maximum turning point.
Date posted: September 11, 2019. Answers (1)
- The figure below shows an arc of a circle through three points A, B and C.(Solved)
The figure below shows an arc of a circle through three points A, B and C.
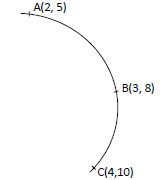
Calculate the co-ordinates of the centre of the circle.
Date posted: September 11, 2019. Answers (1)
- Water flows through a pipe whose cross sectional radius is 3.5cm at a rate of 3m/min.(Solved)
Water flows through a pipe whose cross sectional radius is 3.5cm at a rate of 3m/min. Calculate how long it will take the pipe to fill a 22000 litre Kentank.
Date posted: September 11, 2019. Answers (1)
- The position vectors of points A and B are 2i – j + 4K and 4i + 3j respectively.(Solved)
The position vectors of points A and B are 2i – j + 4K and 4i + 3j respectively. If point R is the midpoint of AB . Find the magnitude of AR
Date posted: September 11, 2019. Answers (1)
- A Kenya airways plane flies from point P(40°N, 45°W) to a point Q(35°N, 45°W), then to point T(35°N, 135°E). Find the shortest distance between Q...(Solved)
A Kenya airways plane flies from point P(40°N, 45°W) to a point Q(35°N, 45°W), then to point T(35°N, 135°E). Find the shortest distance between Q and T in nautical miles.
Date posted: September 11, 2019. Answers (1)
- Solve for x in the equation sin2 (3x + 30°) (Solved)
Solve for x in the equation 
Date posted: September 11, 2019. Answers (1)
- The product of the digits in a two digit number is 24. Four times the ten digit exceeds the unit digit by
10. Calculate the number(Solved)
The product of the digits in a two digit number is 24. Four times the ten digit exceeds the unit digit by
10. Calculate the number
Date posted: September 11, 2019. Answers (1)
- The figure below drawn to scale represents a field in the shape of an equilateral triangle of sides 120m.(Solved)
The figure below drawn to scale represents a field in the shape of an equilateral triangle of sides 120m.
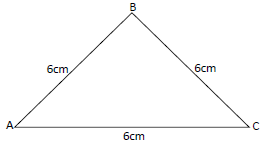
Mr. Mutai wants to plant some tea seedlings in the field. The seedling must be at most 90m from A and nearer to B than to C. If no seedling is to be more than 60m from BC, show by shading, the exact region where the seedling may be planted within the triangle.
Date posted: September 11, 2019. Answers (1)
- The equation of a curve is y = x³ - 3x² + Kx + 2 and a normal is 9y + x = 18.(Solved)
The equation of a curve is y = x³ - 3x² + Kx + 2 and a normal is 9y + x = 18. If they intersect at x = 0; Find the value of K.
Date posted: September 11, 2019. Answers (1)
- A commercial plot is valued at shs.500,000. The plot depreciates at a rate of 10% per six months for a period of 2 years.(Solved)
A commercial plot is valued at shs.500,000. The plot depreciates at a rate of 10% per six months for a period of 2 years. It then appreciates at a rate of 4% per quarter yearly for three years. Find the value of the plot after 5 years to nearest shillings.
Date posted: September 11, 2019. Answers (1)
- Hence use the expansion to evaluate (3.25)5 correct to 4 decimal places.(Solved)
Expand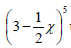 
up to the 5th team. Hence use the expansion to evaluate (3.25)5 correct to 4 decimal places.
Date posted: September 11, 2019. Answers (1)
- Make P the subject of the formula:(Solved)
Make P the subject of the formula:
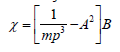
Date posted: September 11, 2019. Answers (1)