- A triangle T whose vertices are A (2,3) , B (5,3) and C (4,1) is mapped onto triangle T(Solved)
A triangle T whose vertices are A (2,3) , B (5,3) and C (4,1) is mapped onto triangle T whose vertices are A1 (-4,3), B1 (-1,3) and C1 (x, y) by transformation
(a) Find the
(i) Matrix M of transformation.
(ii) Find the coordinates of C
(b) Triangle T2 is the image of triangle T1 under a reflection in the line y = x. Find single matrix that maps T onto T2
(c) Find the coordinates of T2
Date posted: September 11, 2019. Answers (1)
- The quantities p and r are connected by the equation p = krn. The table of values of p and r is
Given below.(Solved)
The quantities p and r are connected by the equation p = krn. The table of values of p and r is
Given below.
(a) State a linear equation connecting p and r.
(b) Using the scale 2cm to represent 0.1 units on the y – axis and 1cm rep 0.1 units on the x – axis, draw a suitable line graph on the grid provided.
(c) Hence estimate the value of k and n
(d) Find the law connecting p and r
Date posted: September 11, 2019. Answers (1)
- (a) Complete the table below for the functions y = 2 Cos x and y = sin 2x (Solved)
(a) Complete the table below for the functions y = 2 Cos x and y = sin2x for -180º ≤ x ≤ 180º
(b) On the grid provided, draw on the same axis the graphs of y = 2cos x and y sin 2x for -180º ≤ x ≤ 180º
(c) Use the graphs in (b) above to find;
(i) The values of x such that 2 cos x - sin 2x = 0
(ii) State the amplitude and period of graph y = 2 cos x.
(iii) Find the difference in the value of y when x = - 450
Date posted: September 11, 2019. Answers (1)
- The taxation rate for 2007 were as in the table below.(Solved)
The taxation rate for 2007 were as in the table below.
In certain month in 2007, Ekachoro paid a tax of ksh.3000 after having been given a personal relief ksh.1056 per month.
(a) How much tax per month could he have paid if he did not get tax relief.
(b) Calculate his total taxable income in ksh. P.M.
(c) Given that his total taxable allowance amount to ksh.4520 p.m. Calculate his monthly basic salary in Kenya shillings.
Date posted: September 11, 2019. Answers (1)
- Given the co-ordinates of a point P is (-1, 3, 5) and Q is (2, -2, 4).(Solved)
Given the co-ordinates of a point P is (-1, 3, 5) and Q is (2, -2, 4). Find
(a) PQ in terms of i, j and k
(b) /PQ/
Date posted: September 11, 2019. Answers (1)
- Using a ruler and pair of compass only construct :
(a) An equilateral triangle ABC of side 6cm(Solved)
Using a ruler and pair of compass only construct :
(a) An equilateral triangle ABC of side 6cm
(b) The focus of a point P inside the triangle such that AP < or equal to PB
(c) The locus of a point Q such that AQ > 4cm
(d) Mark and label the region x inside the triangle which satisfy the two loci.
Date posted: September 11, 2019. Answers (1)
- Find the values of p and q.(Solved)
Given the recurring decimal 
is equivalent to p/q where p and q are integers.
Find the values of p and q.
Date posted: September 11, 2019. Answers (1)
- Find A1B-1(Solved)
find A1B-1
Date posted: September 11, 2019. Answers (1)
- Fullmera bought maize and beans from Okame. She mixed the maize and beans in the ratio 3 : 2(Solved)
Fullmera bought maize and beans from Okame. She mixed the maize and beans in the ratio 3 : 2 she bought the maize at sh.90 per kg and the beans at sh.150 per kg. If she was to make a profit of 30% what would be the selling price of 1kg of the mixture.
Date posted: September 11, 2019. Answers (1)
- Solve the equation 4 cos2 theta + 3 sin theta = 4(Solved)
Solve the equation 4 cos2 theta + 3 sin theta = 4 
Date posted: September 11, 2019. Answers (1)
- The data below shows the age of 10 students picked at random in a secondary school(Solved)
The data below shows the age of 10 students picked at random in a secondary school
6, 11, 13, 14, 8, 7, 12, 20, P and 9. If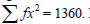 
,determine the value of P hence, find the standard deviation to 3 d.p
Date posted: September 11, 2019. Answers (1)
- Expand (2 – x)6 in ascending power of x.(Solved)
Expand (2 – x)6 in ascending power of x. Use the first four terms of expansion to solve (1.95)6 Correct to four decimal places.
Date posted: September 11, 2019. Answers (1)
- A quantity P varies jointly as Q and the square of R. If Q increased by 20% and R decreased by 15%.(Solved)
A quantity P varies jointly as Q and the square of R. If Q increased by 20% and R decreased by 15%. Find the percentage change in P.
Date posted: September 11, 2019. Answers (1)
- The top of a table is a regular hexagon. Each side of the hexagon measures 50.0cm. (Solved)
The top of a table is a regular hexagon. Each side of the hexagon measures 50.0cm. Find the Maximum percentage error in calculating the perimeter of the top of the table.
Date posted: September 11, 2019. Answers (1)
- The number line shows an integer operation whose result is 7.(Solved)
The number line shows an integer operation whose result is 7.
Write down the actual operation.
Date posted: September 11, 2019. Answers (1)
- Given that tan 650 = 3 + v5 , without using tables or calculator, determine tan 250(Solved)
Given that tan 650 = 3 + √5 , without using tables or calculator, determine tan 250, leaving your answer in the form at a + b √c where a, b and c are rational numbers.
Date posted: September 11, 2019. Answers (1)
- Solve for x in the equation log8 (x + 5) – log8 (x – 3) = 2/3(Solved)
Solve for x in the equation log8 (x + 5) – log8 (x – 3) = 2/3
Date posted: September 11, 2019. Answers (1)
- Make b the subject of the formula.(Solved)
Make b the subject of the formula.
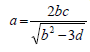
Date posted: September 11, 2019. Answers (1)
- Use logarithms to evaluate correct to 4 s.f(Solved)
Use logarithms to evaluate correct to 4 s.f
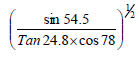
Date posted: September 11, 2019. Answers (1)
- The product of the first three terms of geometric progression is 729.(Solved)
The product of the first three terms of geometric progression is 729. If the first term is a and the common ratio is r.
(a) Express r in terms of a.
(b) Given the sum of the three terms is 39.
(i) Find the values of a and r and hence write down two possible sequences each up to the 4th term.
(ii) Find the product of the 10th term of the two sequences.
Date posted: September 11, 2019. Answers (1)