Find the distance in kilometers between places R(40^oS,25^oW) and S(40^oS,120^oE) along the parallel of latitude(Take radius of the earth to be 6370km and p...

      

Find the distance in kilometers between places R(40^oS,25^oW) and S(40^oS,120^oE) along the parallel of latitude(Take radius of the earth to be 6370km and pi = 22/7) correct to 2 d.p.

  

Answers

---

---

Kavungya answered the question on September 20, 2019 at 06:26

Next: Find the expansion of (1+1/2 x)³ Hence use your expansion to obtain the value of (1.05)³. Correct to 4s.f.
Previous: A coffee trader buys two grades of coffee at sh. 80 and sh. 100 per parket . Find the ratio at which she should mix...

View More Mathematics Questions and Answers | Return to Questions Index

Learn High School English on YouTube

Related Questions

---

• Find the expansion of (1+1/2 x)³ Hence use your expansion to obtain the value of (1.05)³. Correct to 4s.f. (Solved)
  

  Find the expansion of (1+1/2 x)³
  Hence use your expansion to obtain the value of (1.05)³. Correct to 4s.f.

  Date posted: September 20, 2019.  Answers (1)

• The table below shows the marks obtained by Form 3 students of Rehema Secondary School in Mathematics Exam. The total numbers of students were 100.Find...(Solved)
  

  The table below shows the marks obtained by Form 3 students of Rehema Secondary School in Mathematics Exam. The total numbers of students were 100.
  
  
  Find the standard deviation of the distribution.

  Date posted: September 20, 2019.  Answers (1)

• Solve the equation;(Solved)
  

  Solve the equation;
  Log (x²-8x+20) = Log 4 + Log (x-4)

  Date posted: September 20, 2019.  Answers (1)

• Find the matrix of transformation that would map triangle ABC with vertices at A(-5,2), B(-3,2) and C(-3,5) onto triangle A¹B¹C¹ with vertices at A¹(-5,-2), B¹(-3,-2)...(Solved)
  

  Find the matrix of transformation that would map triangle ABC with vertices at A(-5,2), B(-3,2) and
  C(-3,5) onto triangle A¹B¹C¹ with vertices at A¹(-5,-2), B¹(-3,-2) and C¹(-3,-5).
  

  Date posted: September 20, 2019.  Answers (1)

• Rationalize the following leaving your answer in the simplified surd form.(Solved)
  

  Rationalize the following leaving your answer in the simplified surd form.
  

  Date posted: September 20, 2019.  Answers (1)

• If ? is an acute angle find the value of Cos ? in the panating: 4 Sin²?-5 Cos ?+2=0(Solved)
  

  If θ is an acute angle find the value of Cos θ in the panating:
  4 Sin²θ-5 Cos θ+2=0

  Date posted: September 20, 2019.  Answers (1)

• Give that x= 4 is a root of x²+kx-20=0. Find the value of k and thus other roots(Solved)
  

  Give that x= 4 is a root of x²+kx-20=0. Find the value of k and thus other roots

  Date posted: September 20, 2019.  Answers (1)

• Copy and complete the table below for the function y=4+5x-x² for -2=x=7(Solved)
  

  Copy and complete the table below for the function y=4+5x-x² for -2≤x≤7
  

  Date posted: September 20, 2019.  Answers (1)

• A supermarket is stocked with plates which come from two suppliers A and B. They are bought in the ratio of 3:5 respectively, 10% of...(Solved)
  

  A supermarket is stocked with plates which come from two suppliers A and B. They are bought in the ratio of 3:5 respectively, 10% of plates from A are defective and 6% of the plates from B are defective.
  (a) A plate is chosen by a buyer at random. Find the probability that;
  (i) it is from A
  (ii) it is from B and it is defective.
  (iii) it is defective
  (b) Two plates are chosen at random. Find the probability that:
  (i) both are defective
  (ii) at least one is not defective.

  Date posted: September 20, 2019.  Answers (1)

• The points X and Y are both on latitude 39^oN. The longitude of X is 73^oW and the longitude of Y is 18^oW . Two...(Solved)
  

  The points X and Y are both on latitude 39^oN. The longitude of X is 73^oW and the longitude of Y is 18^oW . Two ships P and Q leave X at the same time and travel to Y along the line of latitude. The ships P and Q travel at constant speeds of 25km/hr and 20km/h respectively. Taking the radius of the earth to be 6371km and π= 22/7 ;Calculate:-
  (a) The distance Q still has to travel when P reaches Y.
  (b) At the same time a third ship R leaves Y traveling due west at an average speed of 15km/hr.
  Calculate the longitude of the point at which R meets P.
  

  Date posted: September 20, 2019.  Answers (1)

• In a square PQRS, A is the mid-point of PQ and B is the mid-point of QR, while C is a point on BP such...(Solved)
  

  In a square PQRS, A is the mid-point of PQ and B is the mid-point of QR, while C is a point on BP such that 2BC = 3CP. The co-ordinates of P, Q and S are (4,4), (14,4) and (4,14) respectively. Find:
  (a) (i) the column vectors of PQ and PS.
  (ii) co-ordinates of R
  (b) Show that A, C, S are collinear.

  Date posted: September 20, 2019.  Answers (1)

• The n^th term of a series is given by 3n+4. (a) Write down the first four terms of the series. (b) Find the sum of the first...(Solved)
  

  The n^th term of a series is given by 3n+4.
  (a) Write down the first four terms of the series.
  (b) Find the sum of the first twenty terms of the series.
  (c) Find the 30^th term.
  (d) Show that the sum of the first n terms of the sequence is given by S_n=3/2n²+11/2n. Hence or otherwise, find the largest integral value of n such that Sn ≥130.

  Date posted: September 20, 2019.  Answers (1)

• Find the equation of the tangent to the circle x²+y²-8x+2y+7=0 at the point (3, 2). Give your answer in the form y=ax+b. (Solved)
  

  Find the equation of the tangent to the circle x²+y²-8x+2y+7=0 at the point (3, 2). Give your answer in the form y=ax+b.

  Date posted: September 19, 2019.  Answers (1)

• Without using mathematical tables and calculators simplify:(Solved)
  

  Without using mathematical tables and calculators simplify:
  

  Date posted: September 19, 2019.  Answers (1)

• In the figure below, AB is a tangent, meeting chord CDE at B. DE=xcm Determine: (a) the value of x (b) the length of AB (Solved)
  

  In the figure below, AB is a tangent, meeting chord CDE at B. DE=xcm
  
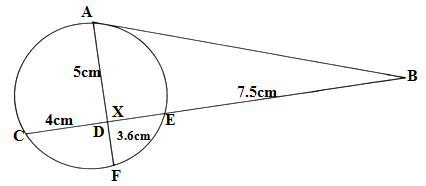
  Determine:
  (a) the value of x
  (b) the length of AB

  Date posted: September 19, 2019.  Answers (1)

• PQRS is a cyclic quadrilateral in which PQ=6cm, QR=2cm, RS=6.5cm, PR=7.2cm and angle PRS=70^o. Determine values of x.(Solved)
  

  PQRS is a cyclic quadrilateral in which PQ=6cm, QR=2cm, RS=6.5cm, PR=7.2cm and angle PRS=70^o.
  
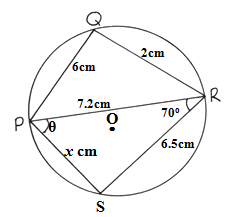
  Determine values of x.

  Date posted: September 19, 2019.  Answers (1)

• Use matrix method to solve simultaneous equations. 3x + 7y = 11 x – y + 4 = 0 (Solved)
  

  Use matrix method to solve simultaneous equations.
  3x + 7y = 11
  x – y + 4 = 0
  

  Date posted: September 19, 2019.  Answers (1)

• The distance between Sotik and Nakuru is 130km. car x starts from Sotik at 8.00 a.m and travels at 40km/hr towards Nakuru. A second car...(Solved)
  

  The distance between Sotik and Nakuru is 130km. car x starts from Sotik at 8.00 a.m and travels at 40km/hr towards Nakuru. A second car y starts traveling from Nakuru at 8.15 a.m towards Sotik at an average speed of 35km/hr. At what time will the two cars meet?

  Date posted: September 19, 2019.  Answers (1)

• A variable P varies as the square of Q and inversely as square root of R. Find the percentage change in P when Q is...(Solved)
  

  A variable P varies as the square of Q and inversely as square root of R. Find the percentage change in P when Q is increased by 5% and R reduced by 19%.

  Date posted: September 19, 2019.  Answers (1)

• Make C the subject of the formula.(Solved)
  

  Make C the subject of the formula.
  

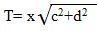
  Date posted: September 19, 2019.  Answers (1)