The figure below is a segment of a circle cut-off by chord AB. Line MX is perpendicular Bisector of chord AB. If AB is 20cm ad...

      

The figure below is a segment of a circle cut-off by chord AB. Line MX is perpendicular Bisector of chord AB.

If AB is 20cm ad MX is 6cm. Calculate the radius of the circle from which the chord was cut.

  

Answers

---

---

Kavungya answered the question on September 23, 2019 at 12:45

Next: Solve the simultaneous equations:
Previous: If Find the values of a, b and c

View More Mathematics Questions and Answers | Return to Questions Index

Learn High School English on YouTube

Related Questions

---

• Solve the simultaneous equations:(Solved)
  

  Solve the simultaneous equations:
  

  Date posted: September 23, 2019.  Answers (1)

• A rectangle has a length of 14.6cm and a width of 6.70 cm. Find the percentage Error in calculating the area of the rectangle.(Solved)
  

  A rectangle has a length of 14.6cm and a width of 6.70 cm. Find the percentage Error in calculating the area of the rectangle.

  Date posted: September 23, 2019.  Answers (1)

• Use Logarithm tables to evaluate(Solved)
  

  Use Logarithm tables to evaluate
  

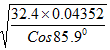
  Date posted: September 23, 2019.  Answers (1)

• Using logarithms, evaluate(Solved)
  

  Using logarithms, evaluate
  

  Date posted: September 23, 2019.  Answers (1)

• Make x the subject of the formula:(Solved)
  

  Make x the subject of the formula:
  

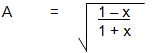
  Date posted: September 23, 2019.  Answers (1)

• Solve the equation(Solved)
  

  Solve the equation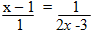

  Date posted: September 23, 2019.  Answers (1)

• Make P the subject of the formula(Solved)
  

  Make P the subject of the formula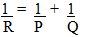

  Date posted: September 23, 2019.  Answers (1)

• The Nyamira Express company runs a fleet of two types of buses operating between Nairobi and Kisii. Type A bus has a capacity of 52...(Solved)
  

  The Nyamira Express company runs a fleet of two types of buses operating between
  Nairobi and Kisii. Type A bus has a capacity of 52 passengers and 200kg of luggage.
  Type B carries 32 passengers and 300kg of luggage. On a certain day, there were 500
  passengers with 3500kg of luggage to be transported. The company could only use a
  maximum of 15 buses altogether.
  a)If the company uses x buses of type A and y buses of type B. Write down all the
  inequalities satisfied by the above conditions.
  b)Draw the inequalities representing the above information
  c)If the cost of running one bus of type A is sh.7200 and that of type B is sh.6000,
  find the minimum cost of running the buses.

  Date posted: September 23, 2019.  Answers (1)

• A particle moves in a straight line with acceleration (5 – 12t) m/s², t seconds after the start. Given that the particle started with a velocity...(Solved)
  

  A particle moves in a straight line with acceleration (5 – 12t) m/s², t seconds after the start.
  Given that the particle started with a velocity of 3m/s.
  a)Find the velocity in terms of t.
  b)Determine the velocity after 2 seconds
  c)Determine the maximum velocity attained by the particle
  d)Calculate the distance covered after one second.

  Date posted: September 23, 2019.  Answers (1)

• In Kemera Secondary school, there are 110 candidates. They sat for a test and scored the following marks a)i)Find the value of X ii)Draw a cumulative frequency...(Solved)
  

  In Kemera Secondary school, there are 110 candidates. They sat for a test and scored the following marks
  
  a)i)Find the value of X
  ii)Draw a cumulative frequency curve representing the information above.
  b)Use the graph to estimate the;
  i)Median
  ii)70^th percentile
  c)If 20% of the candidates passed the test, use the graph to determine the passmark.

  Date posted: September 23, 2019.  Answers (1)

• a)Draw a rectangle PQRS, P(1, 1) Q(4,1), R(4, 3) and S(1, 3) and its image P¹Q¹R¹S¹ under a transformation represented by the matrix. b)P¹Q¹R¹S¹ is mapped...(Solved)
  

  a)Draw a rectangle PQRS, P(1, 1) Q(4,1), R(4, 3) and S(1, 3) and its image P¹Q¹R¹S¹
  under a transformation represented by the matrix.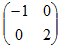
  b)P¹Q¹R¹S¹ is mapped onto P¹¹Q¹¹R¹¹S¹¹ by the matrix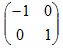
  Draw the image P¹¹Q¹¹R¹¹S¹¹, on the same axes.
  c)Determine the single matrix which maps P¹¹Q¹¹R¹¹S¹¹ onto PQRS
  d)Find the coordinates of P¹¹¹Q¹¹¹R¹¹¹S¹¹¹ the image of P¹¹Q¹¹R¹¹S¹¹ after a reflection in the line y = x.

  Date posted: September 23, 2019.  Answers (1)

• The income taxation table for the year 2010 was as shown; Mr. Ochieng is an employee who earns a basic salary of Ksh.30,000 per month. Other...(Solved)
  

  The income taxation table for the year 2010 was as shown;
  
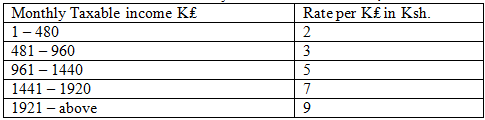
  Mr. Ochieng is an employee who earns a basic salary of Ksh.30,000 per month. Other
  monthly benefits are a house allowance of Ksh.6,000 and commuter allowance of Ksh.3,400.
  He claims a tax relief of sh.1156 per month.
  Calculate
  a)i)His monthly taxable income in K₤
  ii)His monthly net tax
  b)Other deductions per month are:-
  NHIF Kshs.320
  Coop Loan Ksh.5400
  WCPS ksh.300
  Calculate his monthly net salary

  Date posted: September 23, 2019.  Answers (1)

• The figure below shows a cuboid ABCDEFGH. AB = 6cm, BC = 4cm and CG = 8cm. Given that N is the midpoint of EH. Calculate...(Solved)
  

  The figure below shows a cuboid ABCDEFGH. AB = 6cm, BC = 4cm and CG = 8cm.
  Given that N is the midpoint of EH.
  
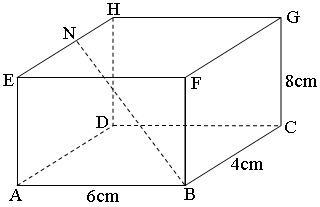
  Calculate the angle between line BN and the base ABCD.

  Date posted: September 23, 2019.  Answers (1)

• Solve the trigonometric equation. Cos 2x = sin x for 0⁰ < x < 360⁰(Solved)
  

  Solve the trigonometric equation.
  Cos 2x = sin x for 0⁰ < x < 360⁰

  Date posted: September 23, 2019.  Answers (1)

• Two points are A(-4, 3) and B(6, -7). A point P moves such that its locus is equidistant from A and B. Find the equation...(Solved)
  

  Two points are A(-4, 3) and B(6, -7). A point P moves such that its locus is equidistant
  from A and B. Find the equation of the locus of P in the form ax + by = c.

  Date posted: September 23, 2019.  Answers (1)

• a)Expand (1 – 2x)¹⁰ up to the 4th term. b)Hence use your expansion in (a) above to evaluate (0.98)¹⁰ correct to 4s.f(Solved)
  

  a)Expand (1 – 2x)¹⁰ up to the 4th term.
  b)Hence use your expansion in (a) above to evaluate (0.98)¹⁰ correct to 4s.f

  Date posted: September 23, 2019.  Answers (1)

• The cost C of operating a computer business is partly constant and partly varies as the square of labour input L. If C = 25,000...(Solved)
  

  The cost C of operating a computer business is partly constant and partly varies as the square of labour input L. If C = 25,000 when L = 20 and C = 45,000 when L = 30. Find C when L = 8.

  Date posted: September 23, 2019.  Answers (1)

• Two lines, x + 2y = -1 and 2x + 3y = 3 intersect at a point P. Find the equation of the circle, Centre...(Solved)
  

  Two lines, x + 2y = -1 and 2x + 3y = 3 intersect at a point P. Find the equation of the circle, Centre P, radius 4 units giving your answer in the form x² + y² + ax + by = c, where a, b and c are constants.

  Date posted: September 23, 2019.  Answers (1)

• The gradient function of a curve is given as 3x² – 4x + 1. If the curve passes through the Point (1, -2). Find the...(Solved)
  

  The gradient function of a curve is given as 3x² – 4x + 1. If the curve passes through the Point (1, -2). Find the equation of the curve.

  Date posted: September 23, 2019.  Answers (1)

• Make S the subject of the formula (Solved)
  

  Make S the subject of the formula
  

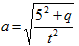
  Date posted: September 23, 2019.  Answers (1)