Solve for x in the equation. 6sin² x - cos x – 5 = 0 for 0⁰ = x = 360

      

Solve for x in the equation.
6sin² x - cos x – 5 = 0
for 0⁰ ≤ x ≤ 360

  

Answers

---

---

Kavungya answered the question on November 6, 2019 at 06:26

Next: The third term and the sixth term of a geometric series are 3 1/3 and 11 1/4 respectively. Calculate the (a) Common ratio (b) First term
Previous: Machine A can complete some work in 8 hours while machine B can complete the same work in 10 hours. The two machines were set...

View More Mathematics Questions and Answers | Return to Questions Index

Learn High School English on YouTube

Related Questions

---

• The third term and the sixth term of a geometric series are 3 1/3 and 11 1/4 respectively. Calculate the (a) Common ratio (b) First term(Solved)
  

  The third term and the sixth term of a geometric series are 3 1/3 and 11 1/4 respectively. Calculate the
  (a) Common ratio
  (b) First term

  Date posted: November 6, 2019.  Answers (1)

• PQ is a diameter of a circle is such that the co-ordinates of P and Q are (-6, -2) and (4, -2) respectively. Find the equation...(Solved)
  

  PQ is a diameter of a circle is such that the co-ordinates of P and Q are (-6, -2) and (4, -2)
  respectively. Find the equation of the circle in the form ax² + by² + cx + dy + e = 0 where a,b,c,d and
  e are constants.

  Date posted: November 6, 2019.  Answers (1)

• Three variables P,Q and R are such that P varies directly as the cube of Q and inversely as the square root of R. If...(Solved)
  

  Three variables P,Q and R are such that P varies directly as the cube of Q and inversely as the square root of R. If Q is increased by 20% and R is decreased by 10%, Find the percentage change in P.

  Date posted: November 6, 2019.  Answers (1)

• Point P(X⁰N, 30⁰E) and Q(X⁰N, 50⁰E) are 1935 km apart. Taking R = 6370km and ?? = 22/7, Find the value of x.(Solved)
  

  Point P(X⁰N, 30⁰E) and Q(X⁰N, 50⁰E) are 1935 km apart. Taking R = 6370km and 𝜋 = 22/7,
  Find the value of x.

  Date posted: November 6, 2019.  Answers (1)

• Make T the subject of the formula(Solved)
  

  Make T the subject of the formula
  

  Date posted: November 5, 2019.  Answers (1)

• Use complete square method to solve for x 8x² + 6x – 9 = 0(Solved)
  

  Use complete square method to solve for x
  8x² + 6x – 9 = 0

  Date posted: November 5, 2019.  Answers (1)

• Find the length of DP in the figure below(Solved)
  

  Find the length of DP in the figure below
  

  Date posted: November 5, 2019.  Answers (1)

• (a) Find the expansion of (1 – x/3 )⁷ in ascending powers of x up to the term in x³. (b) Use the expansion above to...(Solved)
  

  (a) Find the expansion of (1 – x/3 )⁷ in ascending powers of x up to the term in x³.
  (b) Use the expansion above to find, (0.99)⁷ to four significant figures.

  Date posted: November 5, 2019.  Answers (1)

• Solve for x Log₂₇ (x + 5) - log₂₇ (x – 3) = 2/3(Solved)
  

  Solve for x
  Log₂₇ (x + 5) - log₂₇ (x – 3) = 2/3

  Date posted: November 5, 2019.  Answers (1)

• Given that A = 5i + 4j + K and B = 8i – 5j – 5k and P divides AB externally in the ratio...(Solved)
  

  Given that A = 5i + 4j + K and B = 8i – 5j – 5k and P divides AB externally in the ratio 5:2. Find
  the:-
  (a) Position vector of P
  (b) The magnitude of OP

  Date posted: November 5, 2019.  Answers (1)

• Town B is 180km on a bearing 050⁰ from town A. Another town C is on a bearing of 110⁰ from town A and on...(Solved)
  

  Town B is 180km on a bearing 050⁰ from town A. Another town C is on a bearing of 110⁰ from town A and on a bearing of 150⁰ from town B. A fourth town D is 240 km on a bearing of 320⁰ from A. Using scale drawing, such that 1cm rep 30km,
  (a) Show the relative position of the towns
  (b) Using the diagram, find
  (i) Distance AC
  (ii) Distance CD
  (iii) Compass bearing of C from D

  Date posted: November 5, 2019.  Answers (1)

• Nairobi and Eldoret are 600km apart. At 9.20a.m. a lorry leaves Eldoret for Nairobi at a speed of 60km/hr. At 10.00a.m. a car leaves Eldoret...(Solved)
  

  Nairobi and Eldoret are 600km apart. At 9.20a.m. a lorry leaves Eldoret for Nairobi at a speed of 60km/hr. At 10.00a.m. a car leaves Eldoret for Nairobi at a speed of 120km/hr. After 20 minutes of travel, the car develops a mechanical problem which takes 20 minutes to repair. The car then proceeds with the journey at the same speed.
  (a) Calculate the time the lorry arrived in Nairobi
  (b) Find the time when the car overtakes the lorry
  (c) Find the distance from Nairobi at the overtaking point
  (d) Calculate how far the lorry was from Eldoret when the car reached Nairobi

  Date posted: November 5, 2019.  Answers (1)

• Matrix M is given by (a) Find the inverse of M (b) Two schools A and B purchased beans at Ksh. b per bag and...(Solved)
  

  Matrix M is given by
  (a) Find the inverse of M
  (b) Two schools A and B purchased beans at Ksh. b per bag and maize at Ksh. m per bag. School A
  purchased 30 bags of beans and 40 bags of maize for sh. 72,000. School B purchased 50 bags of
  beans and 20 bags of maize for sh. 64,000
  (i) Form a matrix equation to represent the information above
  (ii) Use the inverse matrix of M to find the price of one bag of each item
  (c) The price of beans later went up by 5% and that of maize remained constant. School A bought the
  same quantity of beans but spent the same total amount of money as before on the two items. State
  the new ratio of beans to maize.

  Date posted: November 5, 2019.  Answers (1)

• The figure below shows a square based pyramid on top of a cuboid (a) Draw the net of the solid (b) Calculate the total surface area...(Solved)
  

  The figure below shows a square based pyramid on top of a cuboid
  
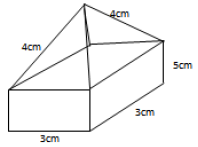
  (a) Draw the net of the solid
  (b) Calculate the total surface area of the net.

  Date posted: November 5, 2019.  Answers (1)

• The gradient function of a curve is given by 3x² + 2x – 3. If the curve passes through the point (-4, -6), Find the...(Solved)
  

  The gradient function of a curve is given by 3x² + 2x – 3. If the curve passes through the point (-4, -6), Find the equation of the curve.

  Date posted: November 5, 2019.  Answers (1)

• The diagram below represents a solid made up of a hemisphere mounted on a cone. The common radius is 6cm and the height of the...(Solved)
  

  The diagram below represents a solid made up of a hemisphere mounted on a cone. The common radius is 6cm and the height of the solid is 15cm.
  
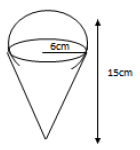
  Calculate the external surface area of the solid

  Date posted: November 5, 2019.  Answers (1)

• Use Logarithms to evaluate(Solved)
  

  Use Logarithms to evaluate
  

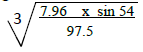
  Date posted: November 5, 2019.  Answers (1)

• Given that sin (3x – 50)⁰ – Cos (x + 20)⁰ = 0 and x is an acute angle; find the value of x(Solved)
  

  Given that sin (3x – 50)⁰ – Cos (x + 20)⁰ = 0 and x is an acute angle; find the value of x

  Date posted: November 5, 2019.  Answers (1)

• Evaluate ; 36^x-1 + 6^2x - 222 = 0(Solved)
  

  Evaluate ; 36^x-1 + 6^2x - 222 = 0

  Date posted: November 5, 2019.  Answers (1)

• The sum of interior angles of a triangle is given by (10x -2y)⁰ while that of a hexagon is given by (30x + 24y)⁰. Calculate...(Solved)
  

  The sum of interior angles of a triangle is given by (10x -2y)⁰ while that of a hexagon is given by (30x + 24y)⁰. Calculate the values of x and y.

  Date posted: November 5, 2019.  Answers (1)