Variance
Variance is the average of the squares of the distance between each value from the mean. The larger the variance, the greater the risk. Variance is calculated as follows;
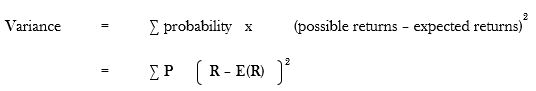
Standard déviation
The standard deviation is the square root of variance. It shows variability of measurements from the mean. It’s calculated as follows;
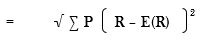
The standard deviation measures how concentrated the data are around the mean; the more concentrated, the smaller the standard deviation. A small standard deviation can be a goal in certain situations where the results are restricted, for example, in product manufacturing and quality control.
But in situations where you just observe and record data, a large standard deviation isn’t necessarily a bad thing; it just reflects a large amount of variation in the group that is being studied. For example, if you look at salaries for everyone in a certain company, including everyone from the student intern to the CEO, the standard deviation may be very large. On the other hand, if you narrow the group down by looking only at the student interns, the standard deviation is smaller, because the individuals within this group have salaries that are less variable. The second data set isn’t better, it’s just less variable.
Coefficient of variation (COV)
This is a measure of relative variability which indicates risk per unit of expected return. It’s determined as follows;
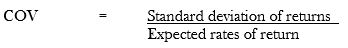
The coefficient of variation allows investors to determine how much volatility, or risk, is assumed in comparison to the amount of return expected from investments. The lower the ratio of standard deviation to mean return, the better risk return tradeoff. Note that if the expected return in the denominator is negative or zero, the coefficient of variation could be misleading.
Lellah answered the question on
November 8, 2021 at 08:40